Based on the Magnetic Resonance Imaging (MRI) technique it is now possible to obtain high resolution brain images reaching scales as low as ~0.2 mm. Diffusion Tensor MRI tomography (DTI-MRI) allows for reconstructing the 3D motion of the water diffusion in the brain area by using the anisoptropic movement of water molecules to capture the positions of the axons connecting the neurons, see Fig. 1 for reconstruction of the neuron axons network from MRI recordings. Based on thorough analysis of MRI images from many healthy brains we have demonstrated self-similarity in the form of a hierarchical architecture of the connectivity matrix of the neuron axons network, which is proper to the healthy state of the brain, while its fractal dimensions were calculated to df~2.5. Using fractal and multifractal analyses we show that these complex connectivity patterns cannot be a result of simple or even chaotic processes because rare, unexpected configurations are present, indicative of the influence of long range exchange mechanisms. A further challenge is to extend the already existing models to cover the cases of pathological brain architectures (Alzheimer, Parkinson and Schizophrenia).

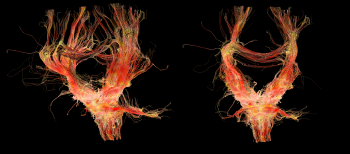
In parallel with the analysis of the detailed structure of the neuron axons network, we use numerical simulations to illustrate brain dynamics, using precise network connectivity matrices as recorded by the MRI analysis. The hierarchical connectivity in the brain, we consider as a key factor for the development of the intricate spatiotemporal patterns covering multiple scales, necessary for the emergence of cognition. Coupling schemes between a large number of neurons follow three main connectivity patterns: all-to-all (global) coupling, nearest neighbours (or local ) coupling and non-local coupling where each neuron is linked with a finite number of neighbours. The last coupling pattern under special conditions produces the so-called ”chimera states”, where some of the oscillators (neurons) oscillate in phase while others are incoherent, see Fig. 2.

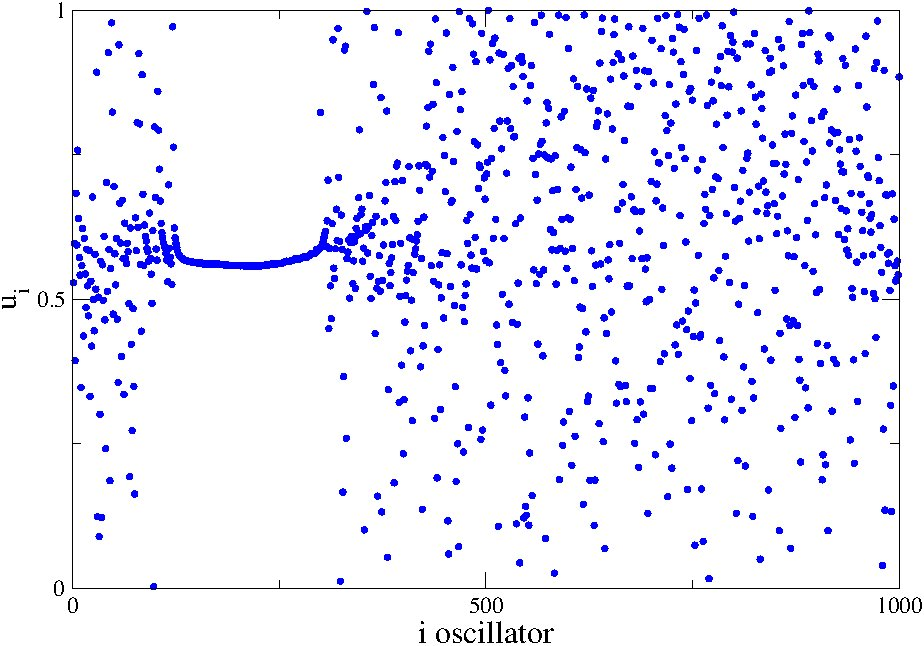
The coexistence of coherent and incoherent states have been associated with partial brain functionality, as in simple brain tasks which engage only a few modules of the brain or in uni-hemispheric sleep. We believe that the presence of chimera states is far more important than proposed for the unihemispheric sleep and is directly related to brain functionality during, at least, simple tasks.

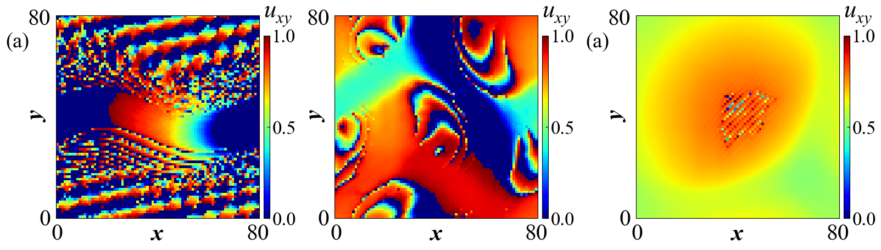
See Related Movies: Chimera States

• Video01.gif : Chimera state on a ring network (1D)  {insert VIDEO: RESEARCH_ACTIVITY01_Computational_Neuroscience_video01.gif  here}
• Video02.mp4 :Chimera state on a 2D torus network with Leaky Integrate-and-Fire dynamics (SPOT)  {insert VIDEO: RESEARCH_ACTIVITY01_Computational_Neuroscience_video02.mp4  here}
• Video03.mp4 : Chimera state on a 2D torus network with Leaky Integrate-and-Fire dynamics (STRIPES) {insert VIDEO: RESEARCH_ACTIVITY01_Computational_Neuroscience_video03.mp4   here}
• Video04.gif : Chimera state on a 2D torus network with Leaky Integrate-and-Fire dynamics (LINES_OF_SPOTS) {insert VIDEO: RESEARCH_ACTIVITY01_Computational_Neuroscience_video04.gif  here}
• Video05.gif : Chimera state on a 2D torus network with Leaky Integrate-and-Fire dynamics (GRID_OF_SPOTS) {insert VIDEO: RESEARCH_ACTIVITY01_Computational_Neuroscience_video05.gif  here}
• Video06.mp4 : Chimera states in Brain Dynamics – Healthy Subject  {insert VIDEO: RESEARCH_ACTIVITY01_Computational_Neuroscience_video06.mp4 here}

Video07.mp4 : Chimera states in Brain Dynamics – Patient with Tumor {insert VIDEO: RESEARCH_ACTIVITY01_Computational_Neuroscience_video07.mp4  here}