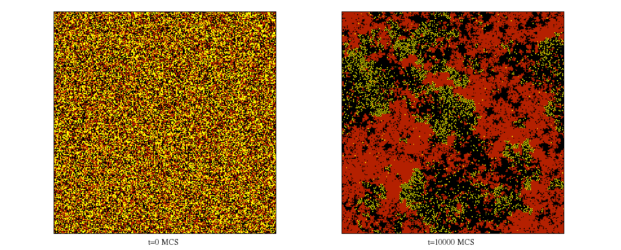
In most systems composed by many interacting elements the activity (dynamics) take place on complex substrates (networks). Common examples are: reaction-diffusion on catalytic surfaces, population dynamics in complex environments, epidemics spreading locally in communities, etc. At the mean-field approximation, when every particle (agent)  in the system interacts with all other particles, the dynamics are described by systems of differential equations (ordinary or partial) and, depending on the complexity of the interactions, the system may reach equilibrium steady states (fixed points), limit cyles,   quasiperiodicity and chaos. When the system is studied beyond the mean field approximation, taking into account local interactions and fluctuations, the spatial restrictions and intrinsic stochasticity change drastically the whole picture. The mean-field dynamics qualitatively remains only under global reactions, while local reactions may drive the lattice to non-equilibrium steady states, including poisoning (where only some of the species survive), Turing pattern formation, patchiness (see Fig. 1) and chimera states (coexistence of synchronous and asynchronous oscillations). Nontrivial oscillatory steady states are developed if long-distance exchange is introduced due to gradual mixing with a certain probability. Kinetic Monte Carlo simulations are employed to describe in detail the local dynamics and the system evolution.   As an example, the mixing probability is shown to control the transition to synchronization which emerges abruptly following a phase slip scenario or a chimera state scenario. The evolution of the process is also drastically affected by the complexity of the network/substrate where the interacting elements are located (see Fig. 2). 

Abstract networks can also be used for the description of the dynamics in reactive processes and they can give valuable information about the evolution and the products of each process. The abstract reactive networks are constructed as follows: The phase space of the variables (concentrations in reactive systems) is partitioned into a finite number of segments, which constitute the nodes of the abstract network. Transitions between the nodes are dictated by the dynamics of the reactive process and provide the links between the nodes. These are weighted networks, since each link weight reflects the transition rate between the corresponding states-nodes. With this construction the network properties mirror the dynamics of the underlying process and one can investigate the system properties by studying the corresponding abstract network. The present construction of abstract networks (based on the partition of the phase space) is generic and can be implemented with appropriate adjustments in many dynamical systems and in time series analysis.

See related videos:  Reaction-Diffusion processes on 2D & 3D supports.

• Video01.avi : The evolution of the Lattice Limit Cycle model (LLC) on a 2D square lattice network. 

 {insert video:  RESEARCH_ACTIVITY02_Reaction_Diffusion_video01.avi here}

• Video02.avi : The evolution of the Lattice Lotka Voltera model (LLV) on a 2D disc lattice network with inhomogeneous initial conditions.

{insert video:  RESEARCH_ACTIVITY02_Reaction_Diffusion_video02.avi here}

• Video03.avi : The evolution of the  Lattice Lotka Voltera model (LLV) on a 3D fractal network.

{insert video:  RESEARCH_ACTIVITY02_Reaction_Diffusion_video03.avi here}