CLOSE

Magnetic Oxides

Manganese perovskites 

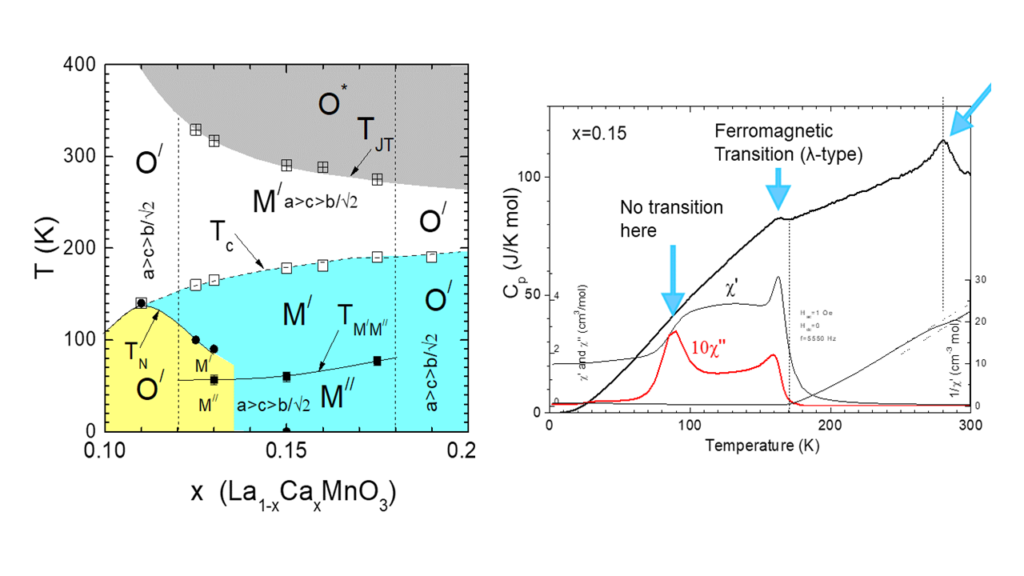
Manganese perovskites with general chemical formula La1-xCaxMnO3 have been thoroughly studied in the past by us, using magnetic, NMR, EPR Mossbauer, x-ray, and neutron data. In this system remain several important non-well understated issues, related with the physics of strongly correlated electrons systems. Below shows a representative specific heat measurement, to understand the nature of the phase transitions observed in the diffraction and magnetization studies. Our measurements have been focused on the ferromagnetic insulated regime, of the magneto-structural phase diagram.  Figure 1 shows the magneto-structural phase diagram, which has been estimated from us using neutron and synchrotron x-ray diffraction data. The left panel of figure 1 shows a representative specific heat measurement of the sample with x=0.15. The data clearly show a λ-type second order transition, coincide with the paramagnetic-canted antiferromagnetic transition detected in magnetization and neutron diffraction data. In the room temperature regime, a symmetric peak is observed, which arises from Janh Teller structural transition. The symmetric peak-shape implies a first order structural phase transition. The anomaly observed around liquid N2 temperatures, in the magnetic measurements, do not show any feature in the specific heat measurements.

Fig. 1 (left upper panel) Part of the magneto-structural phase diagram of the La1-xCaxMnO3 compound in the canted antiferromagnetic -ferromagnetic insulated regime. (right upper panel) Specific heat measurements of the La1-xCaxMnO3 compound, with x=0.15. (lower panel) Unit cell of La1-xCaxMnO3 compound

 Ferrites for microwave and 5G communication systems

Ferrites like Y3Fe5O12, LiFe5O8, is one of the few ferrimagnetic insulators with low microwave losses and high saturation magnetization and Curie temperatures. These properties may be useful in the construction of ultra-wideband photonic devices for 5G communication systems.

Fig. 2 Contour and vector plot of the electric field on the surface of the wave guide, loaded with Y3Fe5O12 ferrite, under a magnetic field kOe, for time phase 0o.The frequency of the ac-electric field was f=14.3 GHz and corresponds to the frequency where the third peak of the transmission coefficient S21 occurs.  The ac-electric field was estimated using ANSYS HFSS (2019 R3).

Fig. 3 Contour and vector plot of the magnetite field on the surface of the wave guide loaded with Y3Fe5O12 ferrite, under a magnetic field kOe for time phase 0o. The frequency of the ac-magnetic field is f=14.3 GHz and corresponds to the frequency where the third peak of the transmission coefficient S21 occurs. The ac-magnetic field was estimated using ANSYS HFSS (2019 R3).
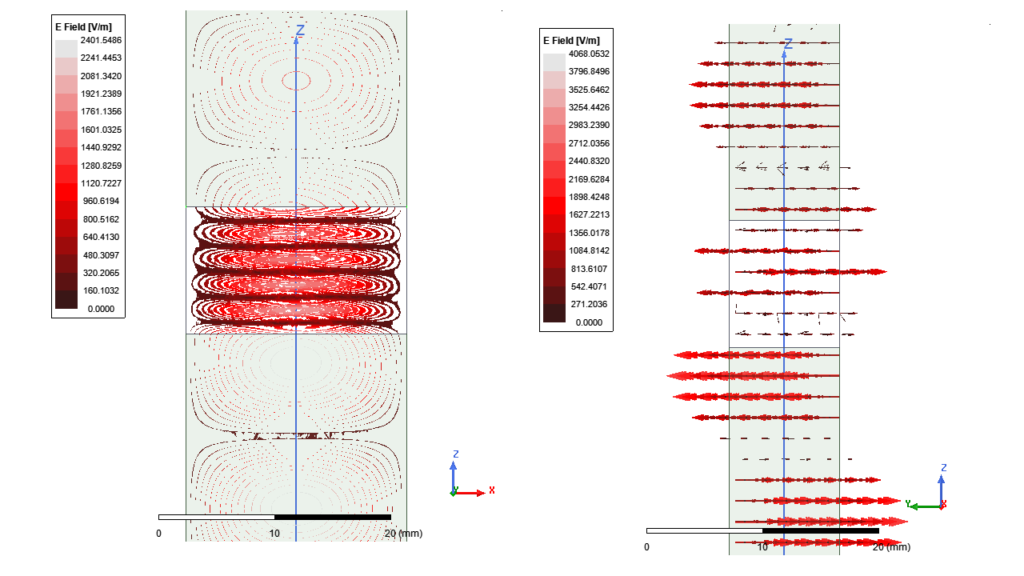
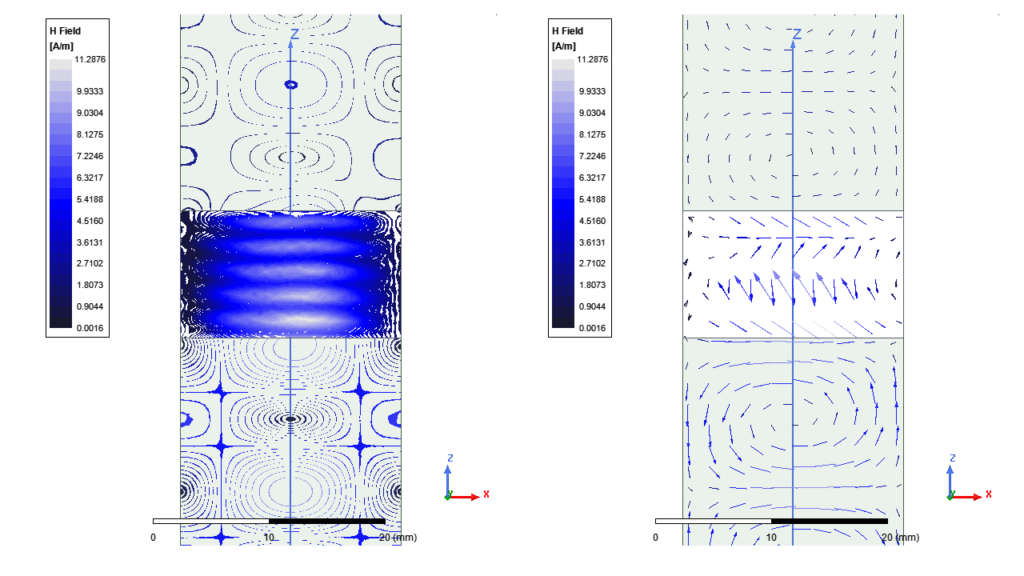
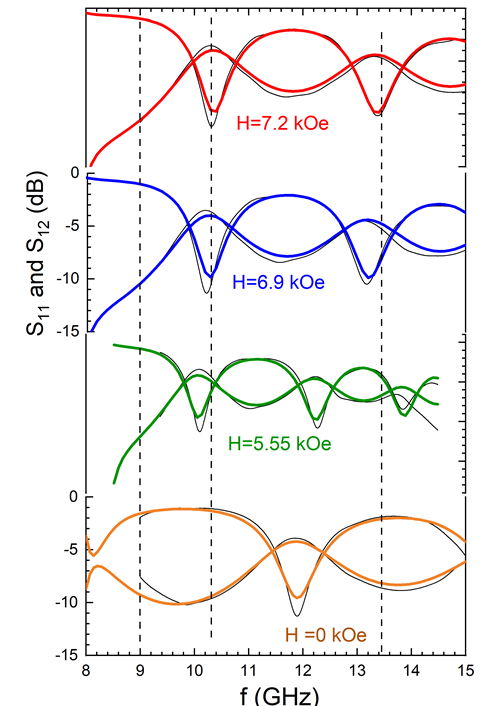
To design these devices, it is necessary to know with high accuracy the material parameters of the ferrites, such the electric permittivity and the parameters of the magnetic permeability tensor. One of the used methods, is the measurement of the scattering parameters of a wave guide filled with a magnetized ferrite. Since it is impossible to calculate theoretically the scattering parameters (S11, S12) and with a fitting procedure to calculate the material parameters, is plausible to resort to a method where the theoretical scattering parameters will be calculated by the numerical solution of the Maxwell equations. To this end we used the ANSYS electromagnetic suite of programs (particularly HFSS, version 2019R3), to calculate the scattering parameters (see fig 2 and 3). By employing a trial-and-error methodology we succeeded to reproduce the experimental scattering parameters, using the same electromagnetic materials parameters for all values of the magnetic field. After few trial simulations we found out that we can have an accepted coincidence between theoretical and experimental scattering parameter, when Oe (see fig4)

Fig. 4 Experimental (thin black lines) and theoretical calculated from the simulation (thick colored lines) scattering parameters S11 and S21 of Y3Fe5O12 ferrite.

Magnetoelectric oxides

The coupling between magnetic and (ferro)electric order is called magnetoelectric effect, which is the induction of magnetization by an electric field or the induction of electric polarization by a magnetic field. The magnetoelectic effect has been studied in the past theoretically by Curie and Dzyaloshinskii

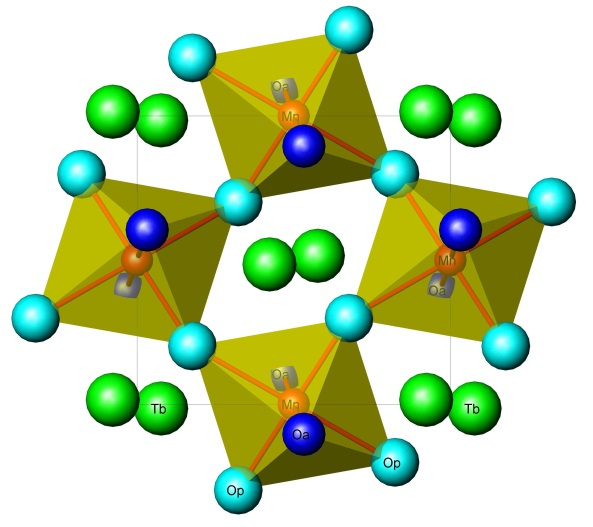
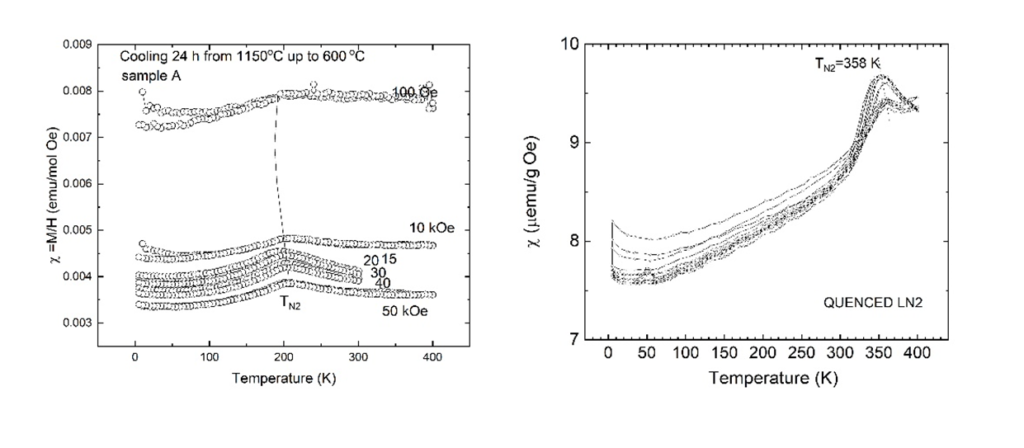
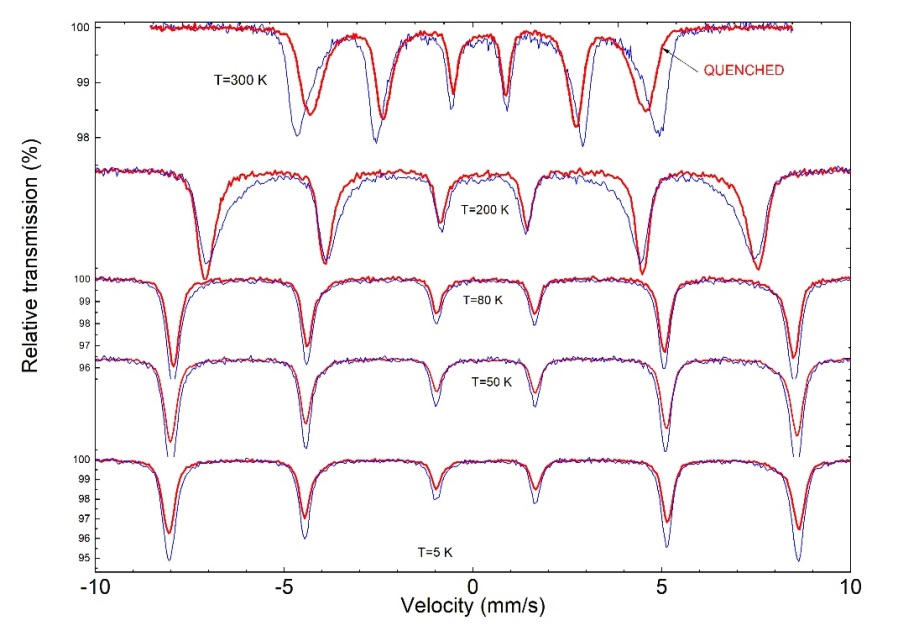
and experimentally by Astrov. The magnetoelectric materials can be used in novel devices, such as computer memories where the magnetic (ferroelectric) domains can be controlled by an electric (magnetic) field, sensors and spintronic devices. The magnetoelectric behavior in existing materials occurs at low temperature and the elements of the magnetoelectric tensor are very small, limiting their practical use. YBaCuFeO5 compound is an antiferromagnetic insulator with Neel temperature around TN=400 K. Below TN2 (depending on the preparation conditions, see Fig. 3) the magnetic structure changes from colinear simple antiferromagnetic to incommensurate magnetic structure (a circular inclined spiral with propagation vectork=(1/2,1/2,1/2 ± q). More importantly an electrical polarization appears below TN2 which scales with the modulus of the magnetic modulation vector q down to the lowest temperature. Our research in this topic is to study the physical origin of the magnetoelectric effect using Mossbauer spectroscopy. Fig. 5 shows representative Mossbauer spectra from two YBaCuFeO5 samples with different incommensurate magnetic transition.

Fig. 5 Temperature variation of the magnetic dc susceptibility of two YBaCuFeO5 samples produced by slowly cooling from 1150oC and quench for 1150oC to LN.

Fig. 6 Mossbauer spectra of YBaFeCuO5 compound produced with slowly cooling (blue spectra) and quenched from 1150oC to LN (red spectra).

The physical origin of the magnetoelectric properties of Y3Fe5O12 ferrimagnetic compound

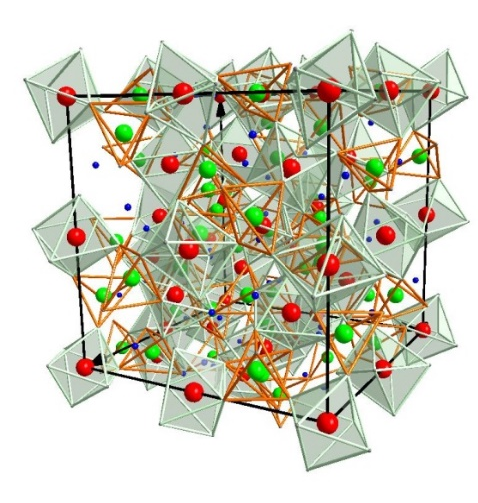
Fig. 7 Unit cell of Y3Fe5O12. YIG crystallizes in cubic system (space group Ia-3d)., The unit cell contains eight formula units. Oxygen anions occupy the general position 96h (x, y, z), Y the dodecahedral 24c (1/8,0,1/4) sites, and Fe occupy two non-equivalent sites [16a (0,0,0) and 24d (3/8,0,1/4)] with octahedral and tetrahedral coordination, respectively.

Y3Fe5O12 (YIG) is a ferrimagnetic prototype compound, displaying interesting physical properties (see Fig.7). This compound has been used in several practical applications such as magnetooptical sensor, microwave ferrite. In recent years intense studies focus on the spin-wave decay length of thin films made from YIG. It was determined to be several centimeters, thus, permitting the spin angular moment to propagate over relatively long distances. This makes YIG an ideal conductor for spin currents transmitted as spin wave excitations. In combination with the spin Hall or inverse spin Hall effect, thin film structures based on YIG could provide a new method to transfer spin information with spin wave excitations. Another important aspect of YIG concerns its magnetoelectric and magneto-capacitive properties, targeting on applications of novel microwave antenna. The magnetoelectric (ME) coupling concerns either a variation of the dielectric response upon application of a variable external magnetic field or a variation of the magnetic response due to electric field variation. The ME properties of YIG have long been under dispute, and its microscopic origin is a long-standing controversy in scientific community. The controversy relies on the physical requirement that a permanent electrical polarization can be observed in materials with non-centrosymmetric crystal structure. So far, all reported crystallographic data on purely stoichiometric YIG cannot provide experimental evidence in support of a non-centrosymmetric center. X-ray linear dichroism data have been reported on epitaxially grown thin films of YIG which are compatible with small structural distortions that make rhombohedral subgroups more realistic, suggesting either a space group R-3 in the ferrimagnetic phase or R3m in the magnetoelectric phase. To elucidate the complex behavior of YIG it is required to understand the puzzling effect of dispersion in electric permittivity and magnetic susceptibility. Our current effort focus on the dielectric and magnetic relaxation effect of YIG samples with different microstructures, employing Mossbauer, x-ray diffraction, scanning electron microscopy, specific heat, magnetic, and dielectric measurements. The obtained results show that dielectric and magnetic relaxation processes appear only for the samples prepared by a solid-state process in our laboratory.
Fig.8 displays the surface morphology observed by SEM on the free surface of pellets from three YIG sample. The first figure corresponds to a commercial sample, displaying low dielectric and magnetic losses. The center and the right picture show the surface morphologies of two YIG samples prepared in our laboratory at 1400oC and 1500oC respectively. The sample prepared at 1400oC display significant dielectric and magnetic losses as well as and magnetoelectric behavior. Interestingly in the sample prepared at 1500oC the electric and magnetic losses are absent. The surface morphology of the commercial sample-reveals polygonal grains of various sizes, with negligibly porosity. The other two samples display significant porosity. The sample prepared in 1500oC displaying a second phase at the grain boundaries.

Fig. 8 Scanning electron photographs of three YIG samples prepared with different conditions. (left photo) Commercial sample. (center) a YIG sample sintered at 1400oC and (right) a YIG sample sintered at 1500oC.

Fig. 9 (left) Mossbauer spectra of the commercial YIG sample. (right) Mossbauer spectra of our sample prepared at 1400oC.

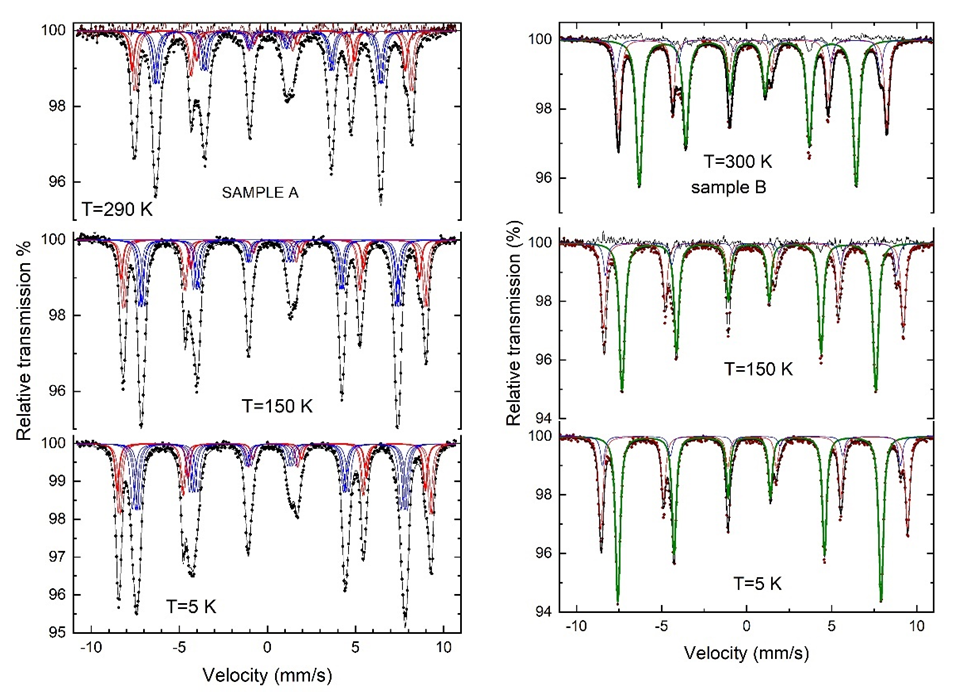
Fig.9 show Mossbauer spectra (MS) collected at 295 K, 150 K and 5 K for the commercial and the prepared in our laboratory YIG samples. These spectra can be analyzed with three partially resolved sextets. The sextet with lower hyperfine magnetic field, is assigned to the tetrahedrally coordinated iron Fe+3, whereas the other two sextets exhibit similar hyperfine magnetic fields and are assigned to octahedrally coordinated Fe+3. Octahedral Fe exhibits two different sextets because each octahedral site has its principal axis of the electric field gradient (EFG) along one of the [111] crystallographic directions, which are the easy directions of magnetization, and the MS are split into two sextets corresponding to two different mutual orientations between the internal field and the principle of the EFG tensor. These two mutual orientations between the EFG z-axis and the direction of hyperfine magnetic field [111] correspond to either an angle Θ=70o or 0o. Thus, the two sextets from octahedral sites can be assigned to nearly similar values of hyperfine magnetic field H. For the tetrahedral site the angle between the principal axis of the EFG sensor and the hyperfine magnetic field is 54o. The main difference between the commercial sample and our sample, is in the pronounced broadening of the tetrahedral component. The additional line broadening observed in the MS of the commercial sample was modeled with four sextets with equal magnetic hyperfine field, isomer shift and principal value of the EFG sensor, but different angles between the z-axis of EFG sensor and the hyperfine magnetic field (parallel to the magnetization). This complication supports strongly that this sample either is non-stoichiometric, or the crystal symmetry becomes rhombohedral. The sample prepared in our laboratory, can be fitted with three relative narrow sextets implying that it is stoichiometric, or the rhombohedral distortion is very small.

Skip to content