Superconductivity
Slush vortex mater phase in YBa2Cu3O7 superconductor at tilted magnetic field
The vortex matter in high critical temperature superconductors displays novel phases, mainly due to the increasing role of the thermal fluctuations. The aim of our research effort is to explore unresolved vortex matter issues using high quality single crystals. One of the issues not yet well understood is the slush vortex matter phase. It has been proposed, that this phase exists, above the intersection point between the Bragg glass line and the line of the onset of the peak effect. Figure 1 (left panel) shows the temperature variation of the ac susceptibility, measured under a dc magnetic field H=90 kOe, tilted 30o in respect of the c-axis of the crystal. Our experimental data offer significant evidence that the sharp drop of the χ’ (indicated with arrow if Fig. 1) corresponds to the transmission from the liquid to slush vortex state.

Frequency dependence of the magnetic ac susceptibility in the peak effect region of Ba1-xkxFe2As2 superconductor (superconducting materials)The vortex matter (Abrikosov state) in type II superconductors under the influence of weak pinning centers constitutes an interesting physical system having many similarities with conventional matter. Despite the intensive research effort having been devoted, in studying the vortex matter, the discovery of new superconductors still keeps many surprises and not well understood novel physical effects. One of the most intriguing effect observed in all type II superconductors with weak pinning centers, interesting both from basic physics and applications’ point of view, is the non-monotonous variation of the critical current. In the related literature, this phenomenon is called peak effect (mainly in low-Tc superconductors), second magnetization peak (in high Tc superconductors) or sometimes fishtail effect. Experimentally, the peak effect appears as a diamagnetic negative peak both in dc and ac-susceptibility measurements as a function of temperature, or as non-monotonous variations of the dc-magnetization as a function of dc-magnetic field.

The onset of the peak effect (local minimum of the screening current), relates to the Bragg-glass to vortex glass transition. Mikitik and Brandt using Lindemann type criteria, and the results of the collective pinning theory, estimated the vortex matter phase diagram considering both thermal fluctuations and random point disorder. Usually, the weak frequency dependence of the ac-susceptibility in type II superconductors is related to flux creep of vortices, being a slow process, contrary to the strong frequency dependence predicted for a linear conductor. For Ohmic behavior E=ρJ, the ac-susceptibility is linear and frequency dependent (e.g. max χ''~1/√ω). On the other hand, for a "Bean" superconductor (Ε= E0(J/Jc)n, n>>1) the ac-susceptibility is non-linear and frequency independent. As we see below we have observed a weak frequency dependence of the ac-susceptibility, a fact implying that the departure from the critical state model is small. According to Faraday's law, a frequency change of the external magnetic induction is equivalent with the change of the electric field level developed in the superconductor.Following Brandt's scaling arguments when the superconductor can be described by a power-law current-voltage E~Jn a change of frequency by a factor k and the amplitude of the ac-field by factor k1/n-1 then the susceptibility does not change e.g. χ(f/B01/n-1}). Based on this, one expects that a frequency increasing for constant amplitude of the ac-field leads also, to an increasing of the susceptibility.
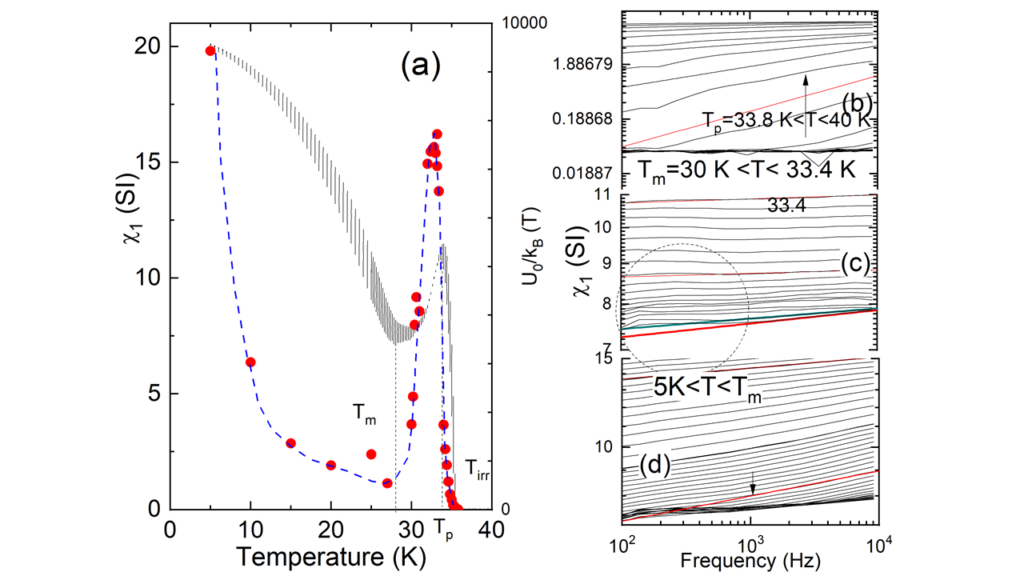
Fig. 3 shows the temperature variation of the fundamental ac-susceptibility χ1, measured under a dc-magnetic field μ0Hdc=7 Tesla and an ac-amplitude of H0=15 Oe for several frequencies.
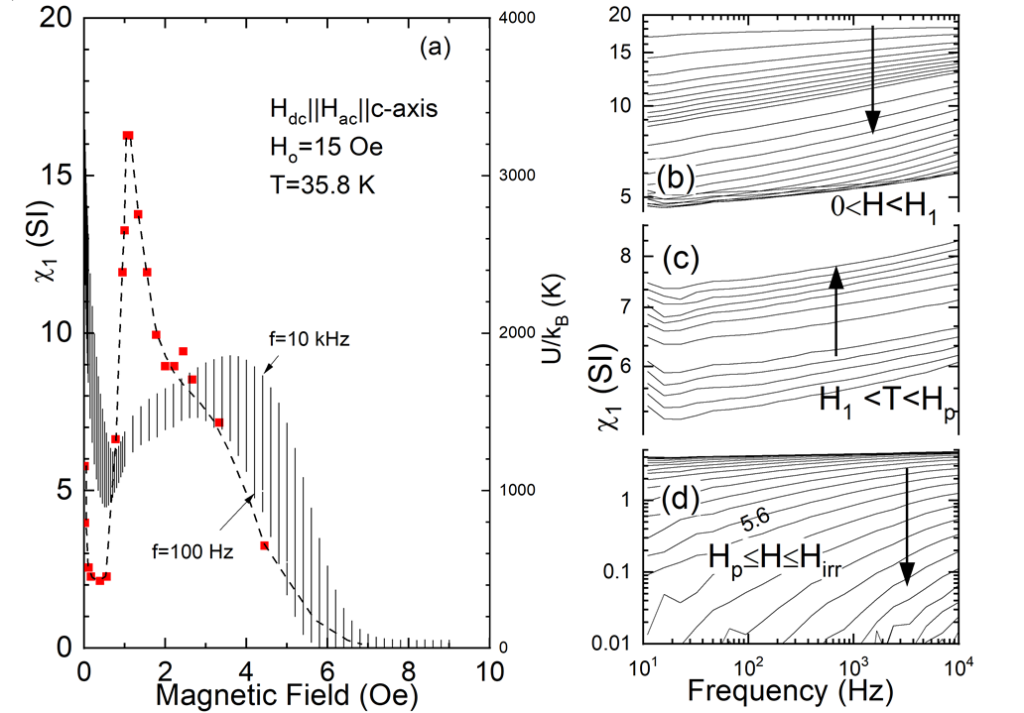
The panels (b), (c) and (d) of Fig.3 show the frequency dependence of χ'1 for constant temperature in double logarithmic plots, in the temperature intervals Tp<T<Tc (panel (b)), Tm<T<Tp (panel (c)) and 5 K< T<Tp (panel (d)), respectively (see Fig.3 for the meaning of Tp, Tm and Tirr). In the temperature interval Tp<T<Tirr, χ'1(f) increases roughly as χ1~fα and shifts nearly parallel as temperature approaches Tp. Below Tp, the frequency dependence is very weak and slightly above Tm, the slope of lnχ’1(f) versus log(f) becomes negative in the range of low frequencies (see region inside dashed circle of Fig. 3. This is an interesting result not predicted from collective creep theory. Finally, for T<Tm, χ’1(f)-curves display again a positive slope in a double logarithmic plot (Fig.3(d)). The absolute logarithmic slope dlogχ’1(f)/dlog(f) gradually increases with temperature, passes through a maximum at around T~ 25 K, and then tends to zero as T⇒ 5 K. Based on the foregoing results we can conclude that ac-respond reveals three dynamic regimes. Fig.4 shows the frequency dependence of the ac-susceptibility for H_0=15 Oe, by varying the dc-magnetic field for constant temperature T=35.8 K. After the Meissner state, where logarithmic rate is zero, it forms a maximum and as H⇒H1 (see Fig. 4(a)) is approached, the slope tends to zero. For H>H1, dlog χ'1(f)/dlog(f) gradually increases. For H>Hp(f=11 Hz) the logarithmic slope increases passes from a maximum and finally becomes zero at Hirr. The data in the particular field regime reveal that the location of the peak effect depends on frequency, e.g. it moves from 2.5 Tesla for f=11 Hz to 3.6 Tesla for f=10 kHz. Since χ' has a monotonous dependence with the critical current, |χ’| should has more or less the same frequency dependence with the critical current. Having found that frequency dependence is roughly a power-law (χ1~fα), we analyzed the data supposing that the exponent is related to an energy barrier throughout the relation $α=kBT/U0, where kB is the Boltzmann's constant. In Fig.3 and Fig.4 a plot of U0 as function of temperature (external magnetic field in Fig. 4) is added (right scale in panels (a)). We keep in mind that although U0 is a phenomenological parameter its temperature dependence reveals the dynamic behavior occurring when the peak effect is observed. It is interesting to note that the peaks of U0(T) and U0(H) curves, both occur below the peak temperature (peak field).
Vortex matter of properties pf K0.8Fe2-ySe2 superconductor
Superconductivity in intercalated iron selenides is an interesting topic, because the physical mechanism being responsible for the superconducting state may be related to the quantum matter issues, topological superconductivity and Majorana zero modes.
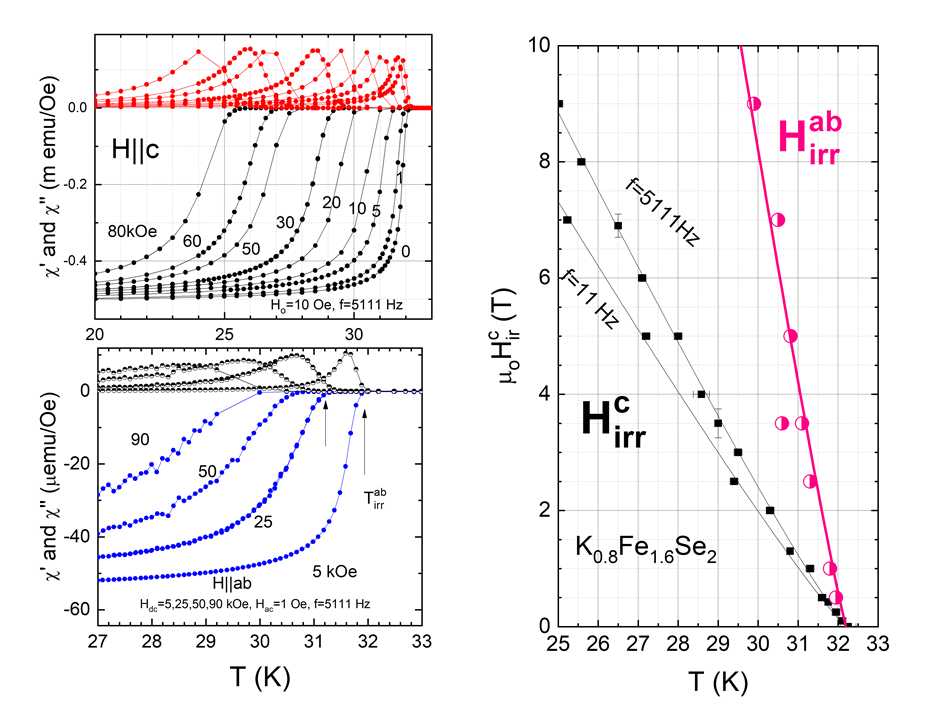
Figure 6 (left panel) shows preliminary results on the vortex matter properties deduced from ac-susceptibility measurements in a K0.8Fe2-ySe2 single crystal for dc magnetic fields (0-9 Tesla), applied parallel to the c-axis and ab-plane. The experimental data were collected using frequencies from 10 Hz up to 10 kHz. From the diamagnetic onset, the irreversibility lines, both for H||c-axis and H||ab-plane, were estimated as a function of temperature and frequency.