ABOUT
The Laboratory of Statistical Mechanics and Dynamical Systems (STAT-DYN) was founded in 02/2004 as part of the former Institute of Physical Chemistry, while from 2014 belongs to the Institute of Nanoscience and Nanotechnology. Its research focuses on theoretical and numerical studies in the domains of :
- Non-linear Dynamics & Statistical Mechanics
- Computational Neuroscience
- Networks of Interacting Neurons & Brain Dynamics
- Complex Networks and their Applications
- Reaction Diffusion Systems
- Fractals, Multifractals and Hierarchical Systems
- Long and Short Range Correlations in Conservative and Dissipative Systems
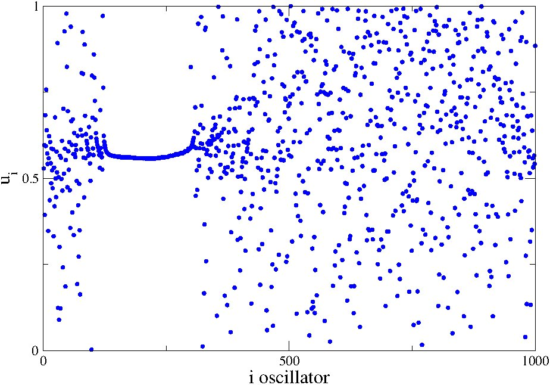
Our aim is the development of methods and models for understanding the emergence and evolution of mesoscopic and macroscopic spatial and temporal patterns and synchronization motifs in networks of interacting elements. A recent example comes from the domain of computational neuroscience: chimera states, which are synchronization motifs in neural networks composed by coexisting synchronous and asynchronous domains, come as a result of cooperation of a large number of interconnected neurons [see Figure01].
A second example comes from the domain of reactive dynamics in hierarchical networks, where nonlinear interactions lead to agrregation phenomena on fractal surfaces [see Figure02].

Other intricate spatiotemporal patterns induced by nonlinear interactions on complex systems/networks include aggregates, spirals and stripe formations, helices, fractals, long and short range correlations and can be experimentally observed in material science, physics, chemistry and biology.
Applications studied in the lab include, among others:
a) In the domain of Computational Neuroscience and Biocomplexity
Numerical simulations of brain dynamics, comparison of dynamics between healthy brains and brains with neurodegenerative disorders, recording and modelling of the complex fractal architecture of the neuron axons spanning the human brain, bioinformatics, DNA complexity and statistical analysis/modelling of cancerous biological tissues.
b) In the domain of Complex Networks and Applications
Reaction-diffusion processes on complex networks, studies of surface phenomena and aggregates with random and fractal morphology, pattern formation in nonlinear dynamics.
Regarding their complexity, natural systems may be categorized in two main classes: closed, conservative systems, and open, dissipative systems, in constant exchange with the environment. In our studies we focus:
- Away from the critical points in closed, isolated, conservative systems, where short range correlations and spatiotemporal patterns with well-defined length and time scales are studied (eg. spiral and stripe formations, helices etc.).
- At the critical points in closed conservative systems, where long range correlations (Levi distributions) are developed and information exchanges extend at long scales.
- In open, coupled dissipative systems the reduction of the phase space is studied, which leads to unexpected spatiotemporal phenomena such as the chimera states in coupled neuronal networks.
For the study of complex dynamical systems in the lab we develop a) statistical methods and algorithms describing the evolution of complex morphologies and b) modelling tools for the dynamics of pattern formation and synchronization phenomena. Statistical methods include thermodynamic approaches, entropic (extensive and non-extensive) approaches, theory of complex networks, theory of long and short range distributions, Levi distributions, theory of random walks. For the study of the mechanisms creating complex patterns, non-linear dynamical systems of hierarchical complexity are used, together with mean-field theories, exact enumeration methods, real-space renormalisation theory, theory of stochastic processes, numerical integration and kinetic Monte Carlo Methods.