CLOSE

AI-Enhanced Computational Nanometrology

In this activity, we focus on the development of mathematical and computational methods including machine learning techniques for the metrological characterization of nanostructure morphologies. The motivation is emanated from the extreme requirements of accuracy on nanoscale which cannot be covered by advances in microscopy hardware only and the increased complexity of nanomorphologies which demands for advanced methods of quantitative characterization. Since plasma technology is used in both well-defined nanopatterns and open (freeform) surfaces, this activity can be separated in two parts:

A. Nanometrology of patterned structures

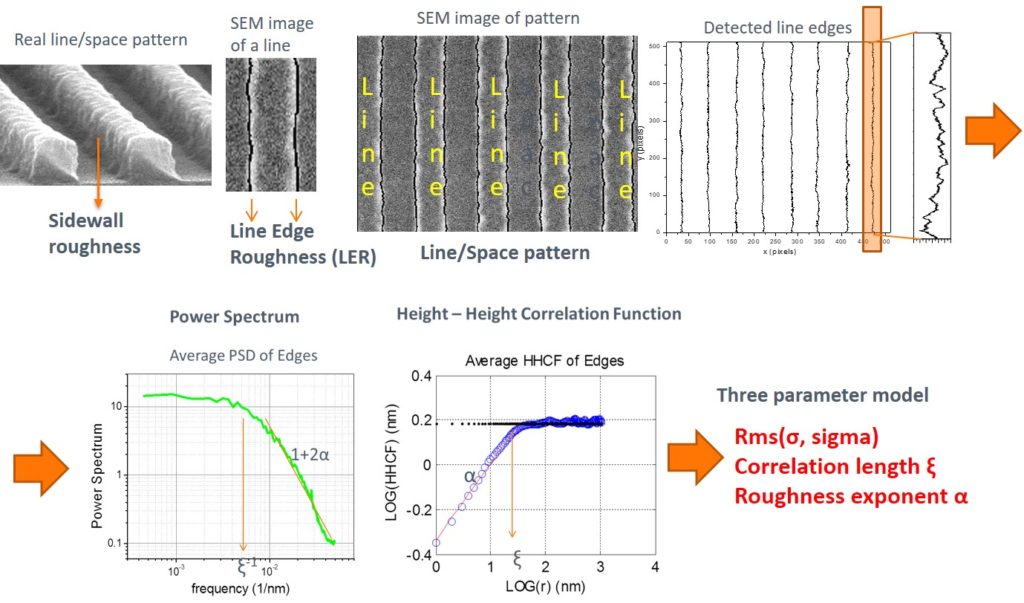
Line Edge Roughness (LER) concerns the sidewall roughness of line/space patterns and is of primary importance in current sub-20nm semiconductor research and industry. During the last two decades, we have pioneered the metrology of LER with the development and application of novel mathematical and computational tools focusing on the spatial and scaling/frequency analysis of LER (including Height-Height Correlation Function (HHCF), Power Spectral Density (PSD), (multi)fractal analysis and the related parameters of the correlation length, roughness exponent and fractal dimension i.e.  the widely accepted and used three-parameter model for LER characterization proposed by our group). Finally, we are a member of the initiative of SEMI standards for the redefinition of the protocol for LER measurement. Our research targets:

A.1 Accuracy issues, such as noise removal from Scanning Electron Microscope (SEM) images

LER is usually measured through the analysis of top-down Scanning Electron Microscope images. However, they suffer from the presence of noise which degrade the accuracy of LER measurements on nanoscale. In order to mitigate noise effects and control their impact, we have developed two strategies. 

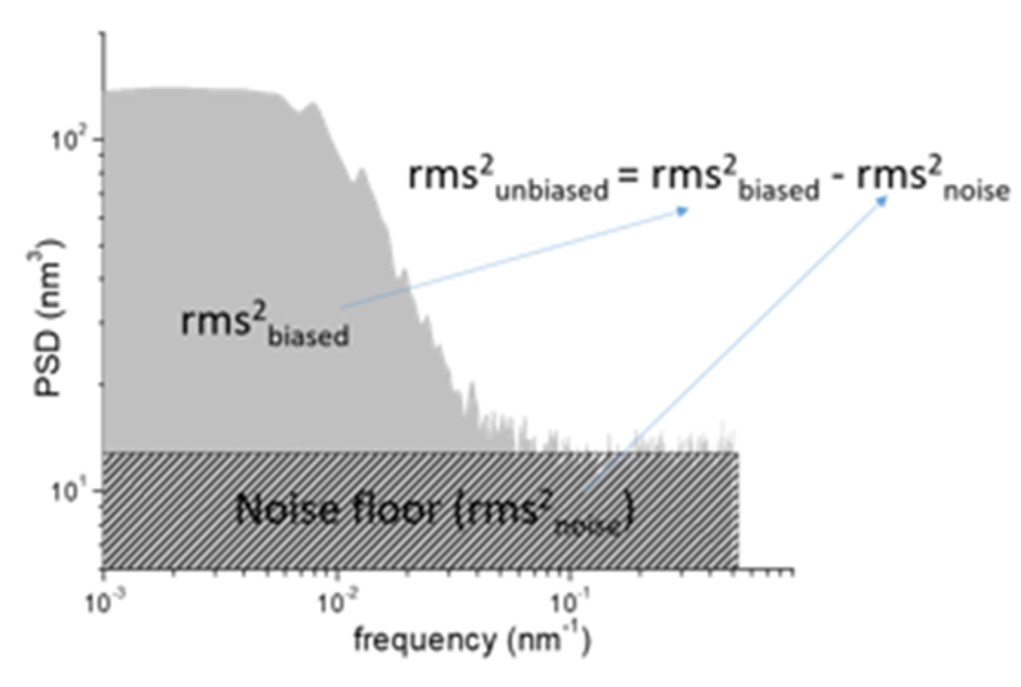
  1. Fourier analysis (Power Spectral Density, PSD) to decompose image noise contribution to LER and acquire unbiased results (see Fig.1) and
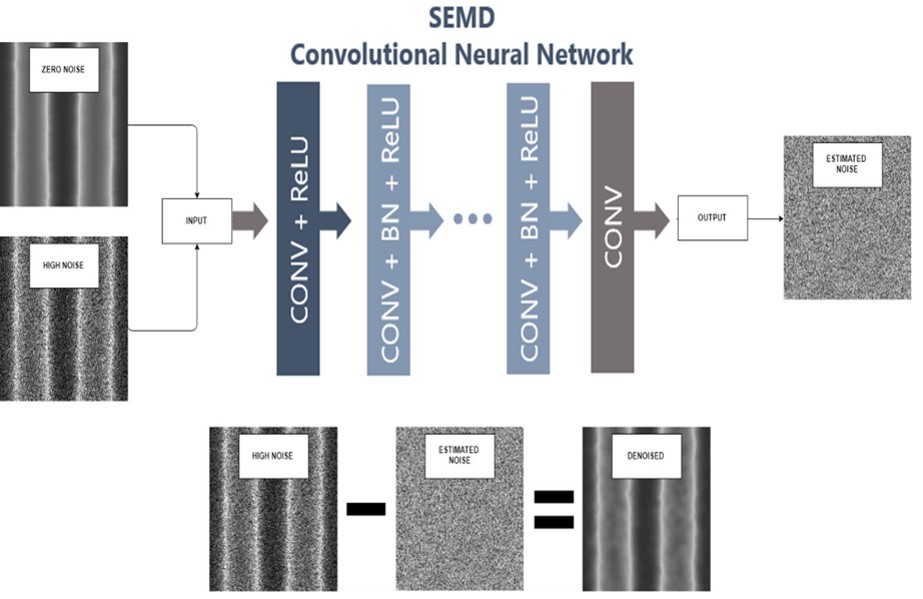
  2. machine/deep learning techniques for the identification of noise effects on the whole image (convolutional neural network) or the edge profile (Hidden Markov Models) and the consequent denoising of images (see Fig.2)

Additionally, we developed a computational modeling to generate computer synthesized grayscale images with controlled levels of noise and LER characteristics. These computer synthesized images imitate closely the real SEM images and are used for validation of PSD-based method and the training of the convolutional neural network and other machine learning models. (see Fig.3). Finally, we have focused on the pixelization effects of SEM images on LER measurement and proposed an approach based on mathematical analysis to remedy these effects and obtain the true LER values.

A.2 Completeness issues such as cross-line correlations, and placement errors

Recently, new challenges in LER metrology have emerged by advances in nanopatterning techniques. In order to address these:

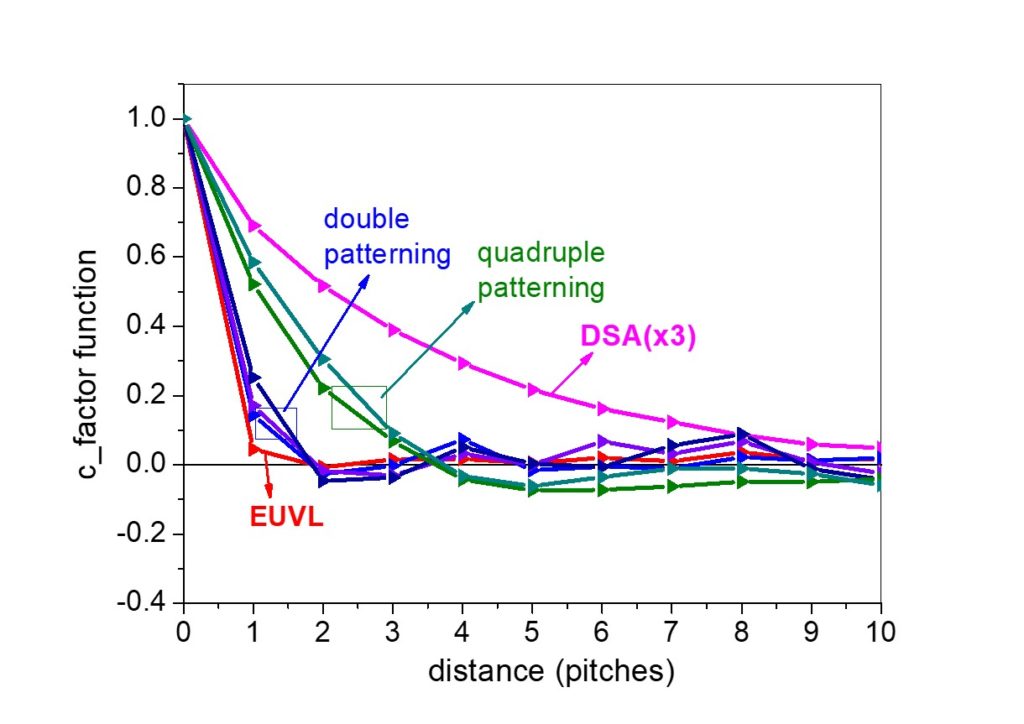
  1. We developed a novel methodology (c-factor correlation function and length) to capture the cross-line correlations critical in patterns with high densities (small pitch) and those produced by Directed Self-Assembly and Multi-Patterning lithographies. (see Fig.4)
  2. We initiated a hierarchical approach for the mathematical characterization of a real pattern targeting the identification of the two scales (pitch and CD) defining the line patterns and the two directions (across and along line direction) that correlations and deviations can appear.
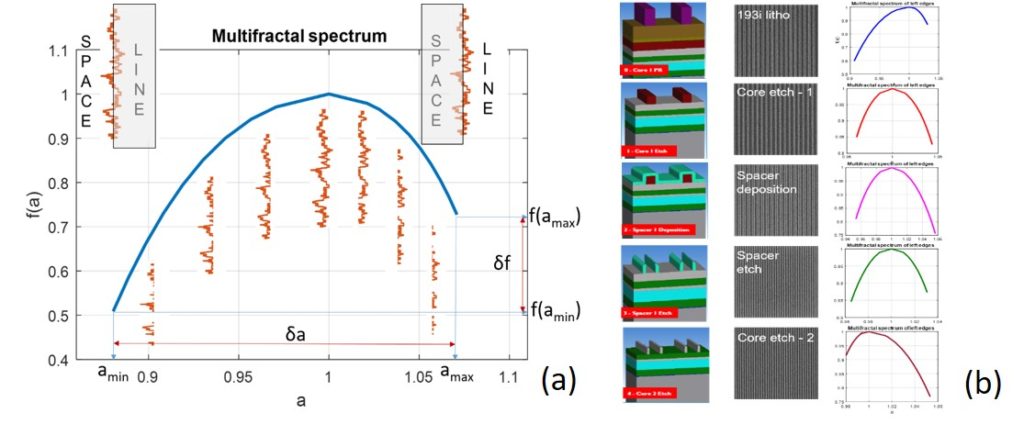
  3. We applied the multifractal analysis properly adapted in LER characterization. (see Fig.5)

We work on Edge and Pattern Placement Error and its relation with LER, targeting design rules of modern circuits taking LER into account.

Fig.1. LER is the sidewall roughness of line/space patterns as displayed in top-down SEM images. Here, we show the steps of LER extraction starting from the initial pattern, the top-down SEM image and the detected edges of lines along with the basic metrics for its quantitative characterization (Power Spectral Density – PSD, Height-Height Correlation Function – HHCF and the three-parameter model).

Fig.2. The PSD-based method for noise-free unbiased measurement of the LER rms value. We allow the presence of noise in edge detection to get a flat floor at high frequencies of the PSD diagram. The area under the flat floor at the whole frequency regime can be used to calculate the contribution of SEM noise to the measured (biased) variance (rms2) of LER. The unbiased rms is then the square subtraction of the noise rms from the measured biased rms.

Fig.3. The architecture of our Deep Learning method (SEMD) based on a convolutional neural network trained to predict the estimated noise of the image from a noisy image. The estimated zero noise image can be calculated by subtracting the estimated residual mapping from the observed high noise image.

Fig.4. Cross-line correlations (quantified by c-factor correlation function) of patterns from different lithographies (Directed Self Assembly – DSA, Extreme UltraViolet – EUVL, double and quadruple patterning) versus distance (measured in pitches). One can notice the sensitivity of c-factor correlation function to the type of lithography and the propagation of line fluctuations across pattern.

Fig.5. (a) A typical example of the multifractal spectrum of real LER (left edges) along with the physical meaning of the left and right branch of the spectrum and the definitions of δa and δf, (b) Multifractal spectra of the LER of line/space patterns during the first five steps of a Quadruple Patterning Lithography process (images from IMEC). Each row shows schematically the pattern and underneath stack (left), a representative top-down SEM image of the pattern (middle) and the multifractal spectrum of the left edges of pattern (right). We can notice the insightful footprint of each process step on the multifractal spectrum (e.g. core etch weakens left branch and strengthen right branch).

B. Nanometrology of open (freeform) complex surfaces

Plasma processing and surface engineering in general produce surfaces with a rich variety and enhanced complexity of  nanomorphologies. The aim of the second part of this activity is to cope with the challenge of the quantification and modeling of complexity and hierarchy in multiscale structures along with methods for the improvement of image quality (see the review paper: Kondi A, Papia E-M, Stai E and Constantoudis V (2025) “Computational methods in nanometrology: the challenges of resolution and stochasticity” Front. Nanotechnol. 7:1559523 doi: 10.3389/fnano.2025.1559523). To this end, we have developed and implemented methods based on

(a) Signal Analysis of Electron and Scanning Probe Microscopy (SM) Images - including Fourier and correlation analysis - enabling three key capabilities:

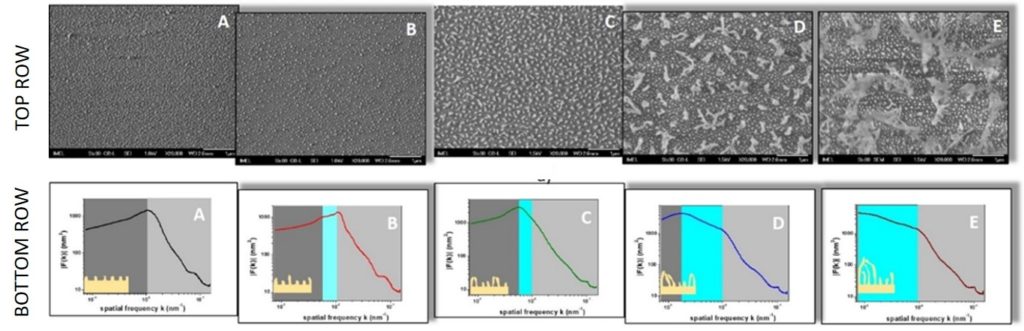
 i) Identification, characterization and modeling of hierarchical surfaces with focus on the cross-scale interactions between hierarchical levels (see Fig.6) (G.Papavieros et.al., 2023 Nanotechnology 34 405702, DOI 10.1088/1361-6528/ace3c8)

ii) Enhancement of image resolution in SM images using the generative Fourier Spectra Stitching (gFSS) method. gFSS method processes a small dataset of images captured at varying magnifications—via electron or scanning probe microscopy—and synthesizes new surfaces that are statistically similar with the input images. The resulting images of surface retain the large field of view of low-magnification image while having the high resolution (small pixel-size) of high-magnification image (see Fig.7) (Stai, E., Constantoudis, V., Kaidatzis, A., Singh, V., Tiwari, M. K., and Gogolides, E. (2025) “Generative resolution-enhanced microscopy based on computational stitching of Fourier spectra” 2025 Micron, 196-197 103867, DOI 10.1016/j.micron.2025.103867)

Fig. 7. (a) Atomic Force Microscope low magnification image of a magnetic (CoFeTa) thin film with pixel size=9.64nm and measurement range 5μm x 5μm, (b) a gFSS-based generated image with the measurement range of low magnification image (5μm x 5μm) of CoFeTa surface and the pixel size of the input high magnification image (1.96nm). The almost five times resolution enhancement of gFSS image is demonstrated by the zoom-ins of both images shown in the insets.

iii) Quantitative characterization of the verticality of nanowires developed on surfaces utilizing the anisotropy of the Fourier spectrum of both top-down and tilted SEM images of the surface to accurately determine whether nanowires are aligned and oriented vertically to the substrate (NWV method). 

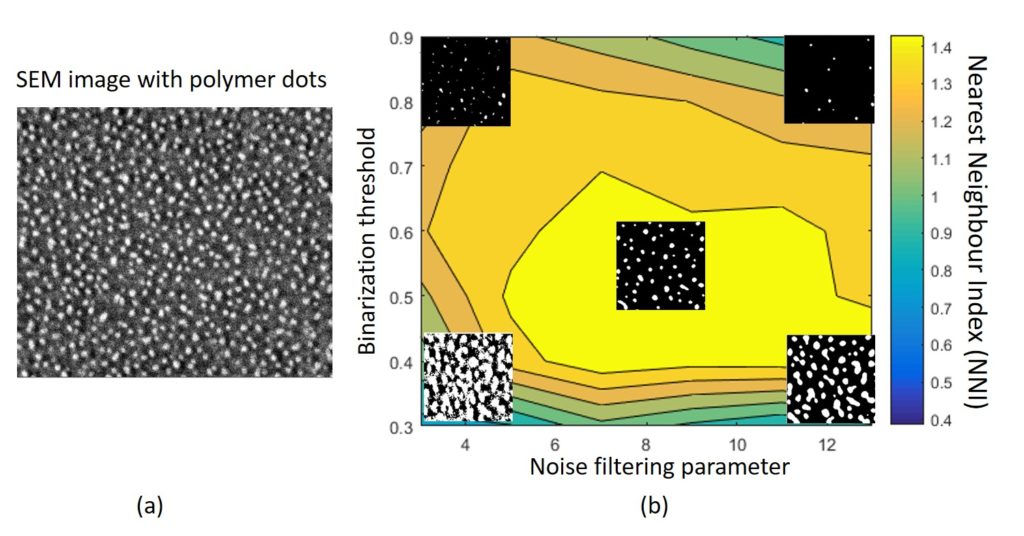
(b) Stochastic geometry (Point Pattern analysis), for the quantification of the extent of order/randomness of the positions of distinct nanostructures (nanoparticles, nanodots, nanowires) on a substrate. Also, the impact of image processing steps (denoising, binarization) on stochastic geometry metrics in real SEM images has been investigated (see Fig.8) (Mavrogonatos, A., Papia, E.-M., Dimitrakellis, P., and Constantoudis, V. (2022) “Measuring the randomness of micro and nanostructure spatial distributions: effects of Scanning Electron Microscope image processing and analysis” J. Microsc. 289, 48–57, doi:10.1111/jmi.13149).

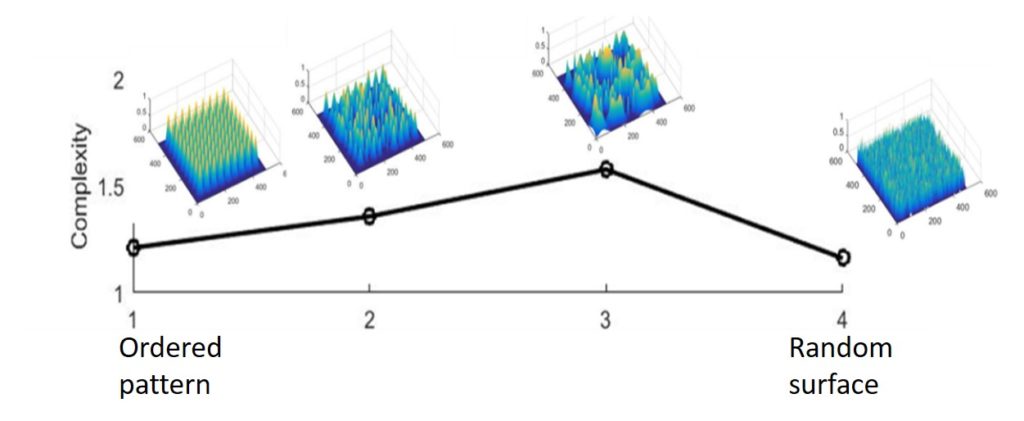
(c) Complexity science (multiscale entropies, chaos-based complexity and multifractality) for measuring the complexity of nanostructured surfaces using the concept of statistical/average symmetry. The concept of multiscale entropy is applied to quantify scale dependent surface heterogeneity, demonstrating that careful histogram binning eliminates amplitude driven distortions and isolates the intrinsic spatial complexity of nanoscale morphologies. As for the chaos-based complexity metric, the key idea is to use chaotic dynamics as a tool for the mixing of pixels of surface microscope images. The surface complexity can then be characterized by the “resistance” of surface morphology to this degradation process and quantified by the inverse of the decay rate of image information loss caused by the chaos-based mixing process.  This idea has been implemented by using the Arnold cat map for the mixing and has been validated on synthetic self-affine and noisy images with controlled correlation length and roughness exponent. It has also applied to SEM images of aluminum surfaces etched in hydrochloric acid for different durations (Kondi, A., Constantoudis, V., Sarkiris, P., Ellinas, K., and Gogolides, E. (2023). Using chaotic dynamics to characterize the complexity of rough surfaces. Phys. Rev. E 107, 014206. doi:10.1103/PhysRevE.107.014206, Arapis, A., Constantoudis, V., Kontziampasis, D., Milionis, A., Lam, C. W. E., Tripathy, A., et al. (2022). Measuring the complexity of micro and nanostructured surfaces. Mater Today Proc. 54, 63–72. doi:10.1016/j.matpr.2021.10.120, Kondi, A.; Constantoudis, V.; Sarkiris, P.; Gogolides, E. Quantifying the Complexity of Rough Surfaces Using Multiscale Entropy: The Critical Role of Binning in Controlling Amplitude Effects. Mathematics 2025, 13, 2325, doi:10.3390/math13152325)

(d) The concept of spatial and structure symmetries. In particular, a symmetry-based analysis has been developed to characterize the deviation of nanostructure morphologies from perfect translational and scaling symmetries (see Fig.9) (V. Constantoudis, I. Ioannou-Sougleridis, A. Dimou, A. Ninou, M. Chatzichristidi, E. Makarona, “A symmetry-based approach to the characterization of complex surface morphologies: Application in CuO and NiO nanostructures”, Micro and Nano Engineering, 16, 2022, 100148, doi:10.1016/j.mne.2022.100148).

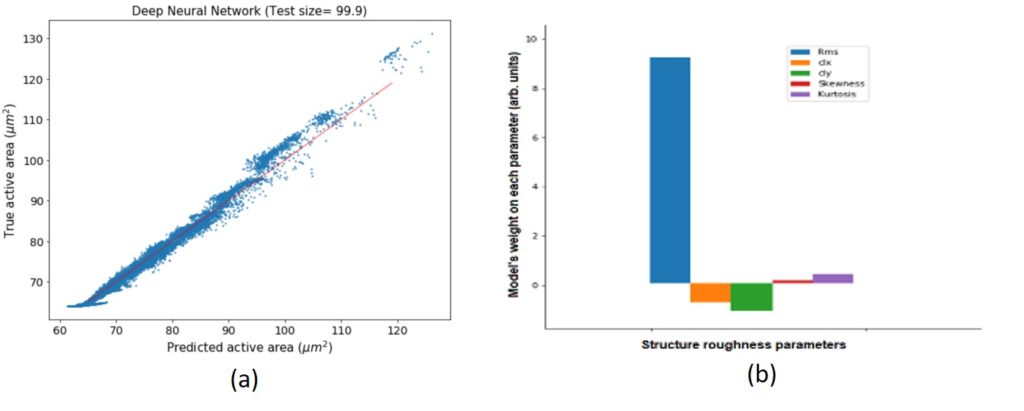
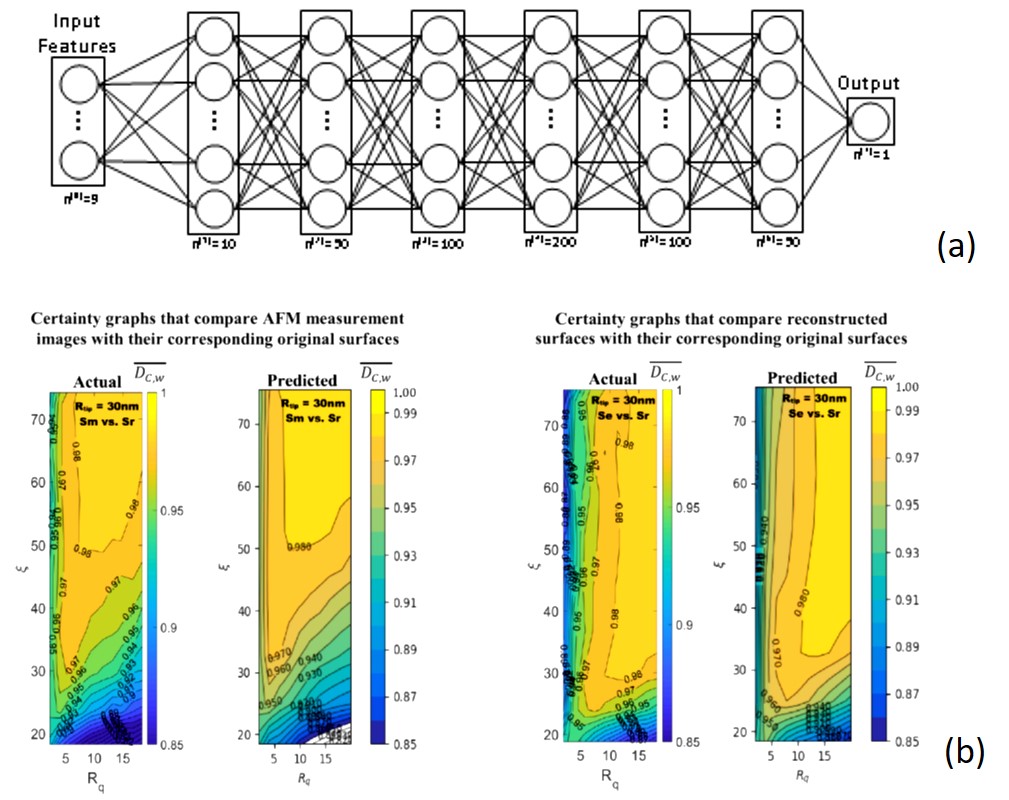
(e) Machine learning (neural networks, random forests) in order to link surface morphology to surface functionality (see Fig.10). Artificial neural networks have also been used to evaluate the importance of tip effects in the accuracy of surface roughness measurement with Atomic Force Microscope (see Fig.11). (Papia, E.-M., Kondi, A., and Constantoudis, V. (2024b). “Inverse design of hexagonal moiré materials: machine learning for tunable pore properties,” in Proceedings of the 13th hellenic conference on artificial intelligence (New York, NY, USA: Association for Computing Machinery). doi:10.1145/3688671.3688744, Kondi, A., Papia, E.-M., and Constantoudis, V. (2024). “Machine learning applications in nanotechnology manufacturing: from etching accuracy to deposition prediction,” in Proceedings of the 13th hellenic conference on artificial intelligence (New York, NY, USA: Association for Computing Machinery), doi:10.1145/3688671.3688740, Efi-Maria Papia, Alex Kondi, Vassilios Constantoudis, Machine learning applications in SEM-based pore analysis: a review, Microporous and Mesoporous Materials, Volume 394, 2025, 113675, doi:10.1016/j.micromeso.2025.113675)

TOP ROW: Top-down SEM images of PMMA surfaces etched by O2 plasma in our new homemade plasma nanotechnology equipment running the “etch-grass” process and having the capacity to control inhibitor flux. The surfaces exhibit a wide diversity of morphologies ranging from single-level (almost periodic) surfaces (A) under limited inhibitor flux, to hierarchical surfaces with varying types of hierarchy (amplitude or spatial) (B-E) induced by the inhibitor deposition with rate increasing from B to E. BOTTOM ROW: The radially averaged Fourier spectra of the SEM images shown in TOP ROW which demonstrate the frequency footprint of hierarchical morphologies as well as the ability of our technique to control the degree (frequency range) of the middle frequency scale of morphological hierarchy.  The insets in the diagrams of Fourier spectra are schematic drawings of the profiles of the etched surfaces to facilitate visualization.

Fig.7. (a) Top-down SEM image of polymer nanodots created after O2 plasma etching for 1min, (b) contour graph illustrating the dependence of the Nearest Neighbour Index (NNI) of nanodot positions on the noise smoothing filter and the binarization threshold needed to detect the dots. One can notice the broad maximum region (yellow area) where NNI gets its maximum value (~1.4) and the identification of nanodots is more accurate. At the four corners of diagram, the nanodot detection is deteriorated as shown in the inset binary images.

Fig.8. The proposed complexity measure versus the randomness of the positions and sizes of Gaussian mounds in a rough surface. One can notice the maximum of complexity measure at the most heterogeneous surface lying between full order and full randomness.

Fig.9. (a) Demonstration of the success of the Deep Neural Network to predict the actual surface area from the values of roughness parameters (Rms, correlation length clx, correlation length cly, skewness, kurtosis) of rough surfaces, (b) the evaluation of the significance of roughness parameters with respect to their impact on active surface area.

Fig.10. (a) Neural Network architecture used to predict the significance of AFM tip effects on the measurement accuracy of surface roughness. The input features may be the roughness parameters (rms Rq, correlation length ξ, fractal dimension, …) and the output result is the measurement certainty quantifying the significance of tip effects (low certainty, large tip effects). (b) Actual certainty graphs (left of each pair) and predicted from the neural network of (a) certainty graphs (right of each pair) for Rtip = 30nm over a range Rq and ξ values for surfaces with Gaussian height distributions. Both certainty graphs include instrumentation noise. One can clearly notice the success of the neural network predictions which can be used to quantify the impact of AFM tip effects and trigger actions for their correction if needed.

C. Nanometrology of fibrous and porous materials

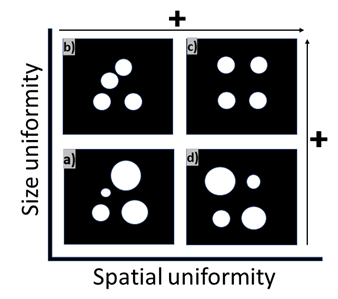
The nanometrology of fibrous and porous materials integrates characterization methods to quantify both size uniformity and spatial uniformity at the nanometer scale (see Fig. 12). Central to this approach is the evaluation of spatial point patterns that characterize the arrangement of pore centroids or fiber junctions within these materials. An analysis tool we employed is the Nearest Neighbour Index (NNI), which allows for precise measurement of the spatial distribution of points (e.g., pores or intersections of fibers). This method provides valuable insight into the aggregation or periodicity of these patterns, revealing essential structural traits that influence material performance. The work lays the foundation for developing tailored porous materials in fields such as membrane filtration, where controlling both size and spatial distribution is key to achieving desired functional properties. (Papia, E.-M., Constantoudis, V., Ioannou, D., Zeniou, A., Hou, Y., Shah, P., et al. (2024a). Quantifying pore spatial uniformity: application on membranes before and after plasma etching. Micro Nano Eng. 24, 100278. doi:10.1016/j.mne.2024.100278, Efi-Maria Papia, Alex Kondi, Vassilios Constantoudis, Machine learning applications in SEM-based pore analysis: a review, Microporous and Mesoporous Materials, Volume 394, 2025, 113675, doi: /10.1016/j.micromeso.2025.113675).

Fig. 12. Schematic representations of 4 simple point patterns as a function of their size uniformity (y axis) and spatial uniformity (x axis). a) Low size uniformity and low spatial uniformity: in this scenario, the pores have varying sizes, and they are distributed unevenly throughout the material, b) high size uniformity and low spatial uniformity: in this case, the pores have consistent sizes, but they are still distributed unevenly throughout the material, c) high size uniformity and high spatial uniformity : the pores have consistent sizes, and they are evenly distributed throughout the material, d) low size uniformity and high spatial uniformity: the pores have varying sizes, but they are distributed evenly throughout the material.

Skip to content