CLOSE

Computational Nanometrology

In this activity, we focus on the development of mathematical and computational methods including machine learning techniques for the metrological characterization of nanostructure morphologies. The motivation is emanated from the extreme requirements of accuracy on nanoscale which cannot be covered by advances in microscopy hardware only and the increased complexity of nanomorphologies which demands for advanced methods of quantitative characterization. Since plasma technology is used in both well-defined nanopatterns and open (freeform) surfaces, this activity can be separated in two parts:

A. Nanometrology of patterned structures

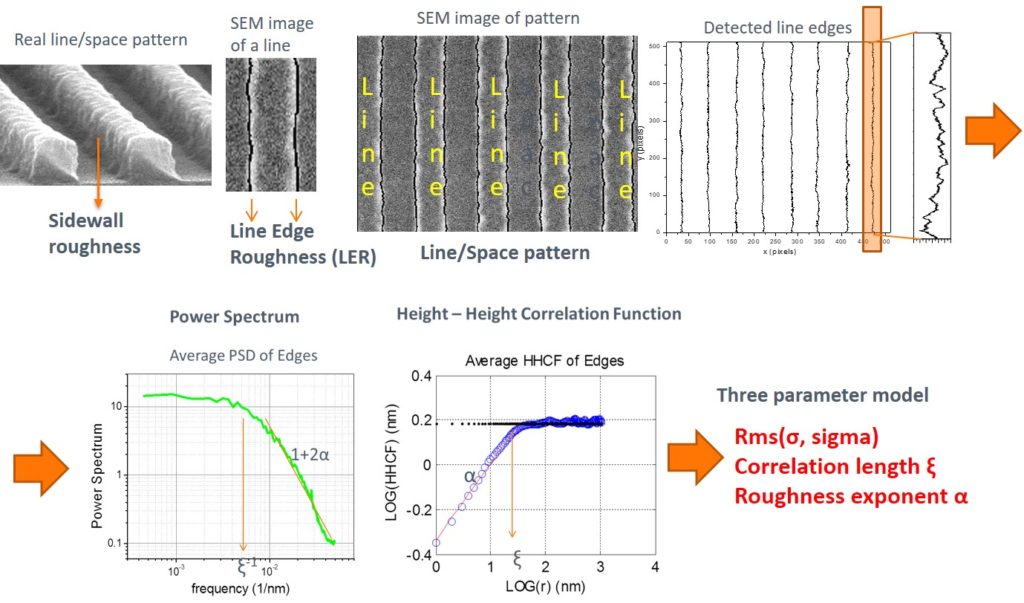
Line Edge Roughness (LER) concerns the sidewall roughness of line/space patterns and is of primary importance in current sub-20nm semiconductor research and industry. During the last two decades, we have pioneered the metrology of LER with the development and application of novel mathematical and computational tools focusing on the spatial and scaling/frequency analysis of LER (including Height-Height Correlation Function (HHCF), Power Spectral Density (PSD), (multi)fractal analysis and the related parameters of the correlation length, roughness exponent and fractal dimension i.e.  the widely accepted and used three-parameter model for LER characterization proposed by our group). Finally, we are a member of the initiative of SEMI standards for the redefinition of the protocol for LER measurement. Our research targets:

A.1 Accuracy issues, such as noise removal from Scanning Electron Microscope (SEM) images

LER is usually measured through the analysis of top-down Scanning Electron Microscope images. However, they suffer from the presence of noise which degrade the accuracy of LER measurements on nanoscale. In order to mitigate noise effects and control their impact, we have developed two strategies. 

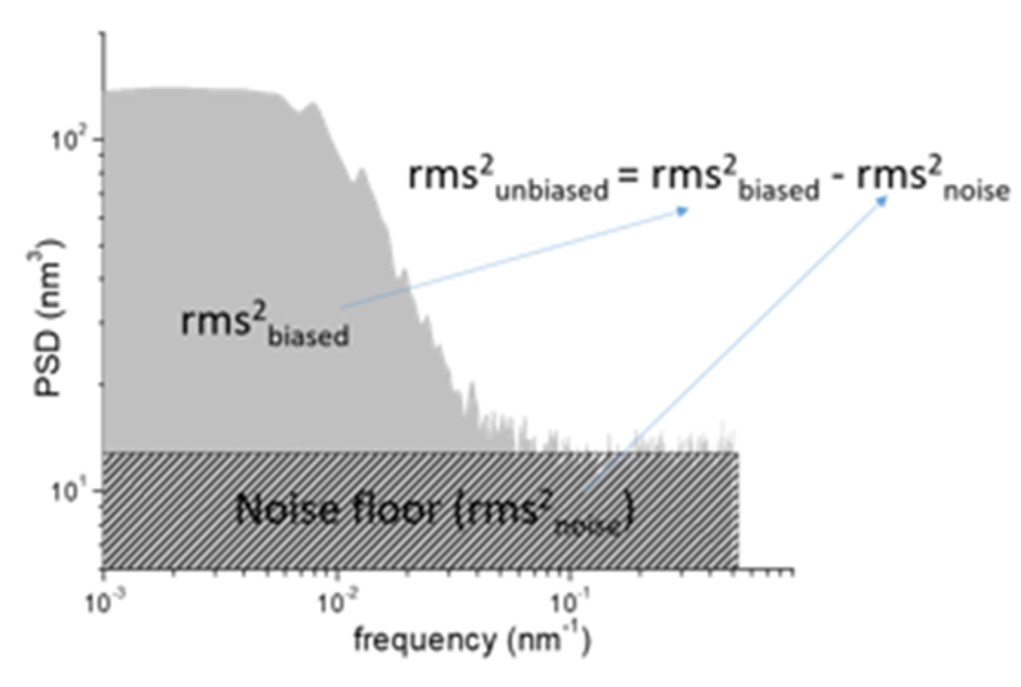
  1. Fourier analysis (Power Spectral Density, PSD) to decompose image noise contribution to LER and acquire unbiased results (see Fig.1) and
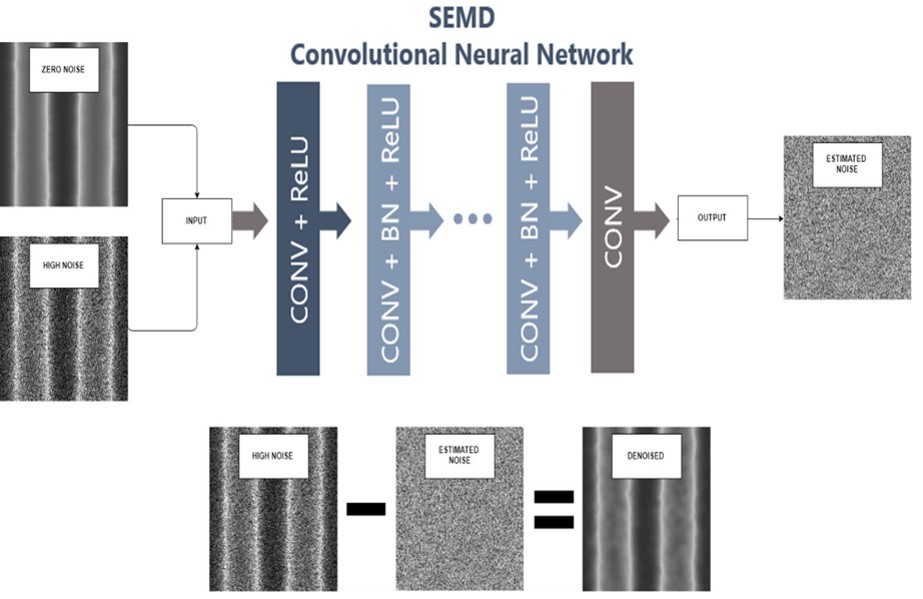
  2. machine/deep learning techniques for the identification of noise effects on the whole image (convolutional neural network) or the edge profile (Hidden Markov Models) and the consequent denoising of images (see Fig.2)

Additionally, we developed a computational modeling to generate computer synthesized grayscale images with controlled levels of noise and LER characteristics. These computer synthesized images imitate closely the real SEM images and are used for validation of PSD-based method and the training of the convolutional neural network and other machine learning models. (see Fig.3). Finally, we have focused on the pixelization effects of SEM images on LER measurement and proposed an approach based on mathematical analysis to remedy these effects and obtain the true LER values.

A.2 Completeness issues such as cross-line correlations, and placement errors

Recently, new challenges in LER metrology have emerged by advances in nanopatterning techniques. In order to address these:

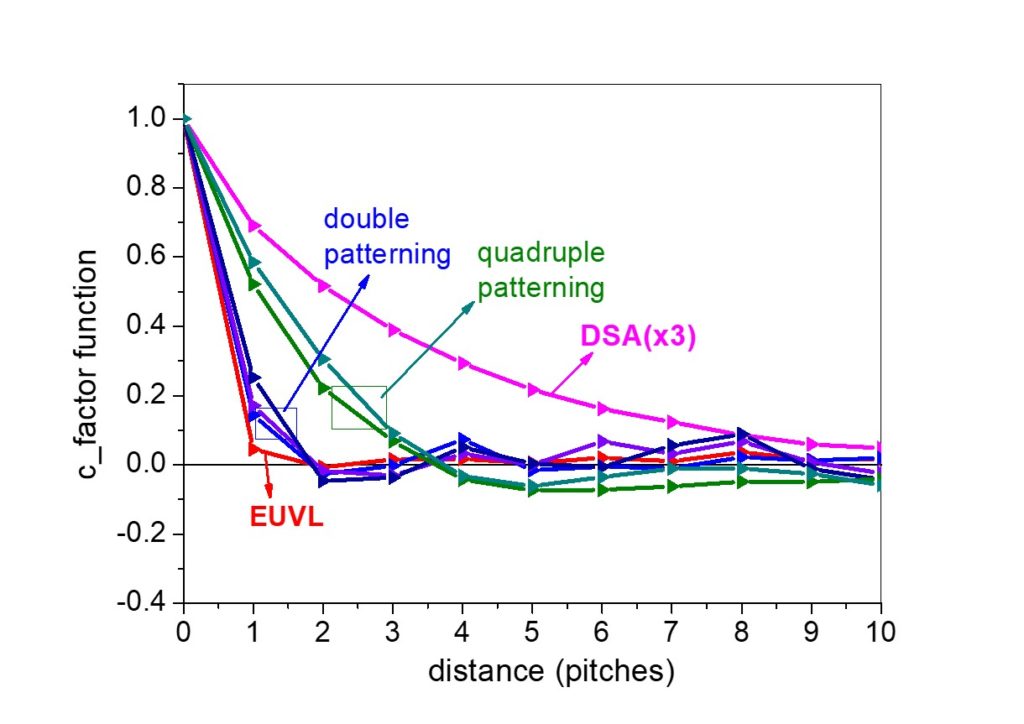
  1. We developed a novel methodology (c-factor correlation function and length) to capture the cross-line correlations critical in patterns with high densities (small pitch) and those produced by Directed Self-Assembly and Multi-Patterning lithographies. (see Fig.4)
  2. We initiated a hierarchical approach for the mathematical characterization of a real pattern targeting the identification of the two scales (pitch and CD) defining the line patterns and the two directions (across and along line direction) that correlations and deviations can appear.
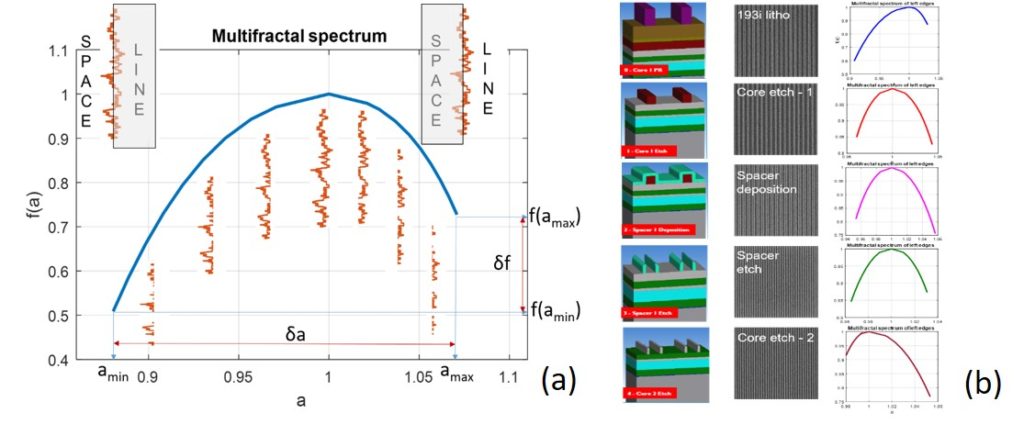
  3. We applied the multifractal analysis properly adapted in LER characterization. (see Fig.5)

We work on Edge and Pattern Placement Error and its relation with LER, targeting design rules of modern circuits taking LER into account.

Fig.1. LER is the sidewall roughness of line/space patterns as displayed in top-down SEM images. Here, we show the steps of LER extraction starting from the initial pattern, the top-down SEM image and the detected edges of lines along with the basic metrics for its quantitative characterization (Power Spectral Density – PSD, Height-Height Correlation Function – HHCF and the three-parameter model).

Fig.2. The PSD-based method for noise-free unbiased measurement of the LER rms value. We allow the presence of noise in edge detection to get a flat floor at high frequencies of the PSD diagram. The area under the flat floor at the whole frequency regime can be used to calculate the contribution of SEM noise to the measured (biased) variance (rms2) of LER. The unbiased rms is then the square subtraction of the noise rms from the measured biased rms.

Fig.3. The architecture of our Deep Learning method (SEMD) based on a convolutional neural network trained to predict the estimated noise of the image from a noisy image. The estimated zero noise image can be calculated by subtracting the estimated residual mapping from the observed high noise image.

Fig.4. Cross-line correlations (quantified by c-factor correlation function) of patterns from different lithographies (Directed Self Assembly – DSA, Extreme UltraViolet – EUVL, double and quadruple patterning) versus distance (measured in pitches). One can notice the sensitivity of c-factor correlation function to the type of lithography and the propagation of line fluctuations across pattern.

Fig.5. (a) A typical example of the multifractal spectrum of real LER (left edges) along with the physical meaning of the left and right branch of the spectrum and the definitions of δa and δf, (b) Multifractal spectra of the LER of line/space patterns during the first five steps of a Quadruple Patterning Lithography process (images from IMEC). Each row shows schematically the pattern and underneath stack (left), a representative top-down SEM image of the pattern (middle) and the multifractal spectrum of the left edges of pattern (right). We can notice the insightful footprint of each process step on the multifractal spectrum (e.g. core etch weakens left branch and strengthen right branch).

B. Nanometrology of open (freeform) complex surfaces

Plasma processing and surface engineering in general produce a rich variety and increased complexity of surface nanomorphologies. The aim of the second part of this activity is to cope with the challenge of the quantification of complexity and hierarchy in multiscale structures. To this end, we have developed and implemented methods inspired by 

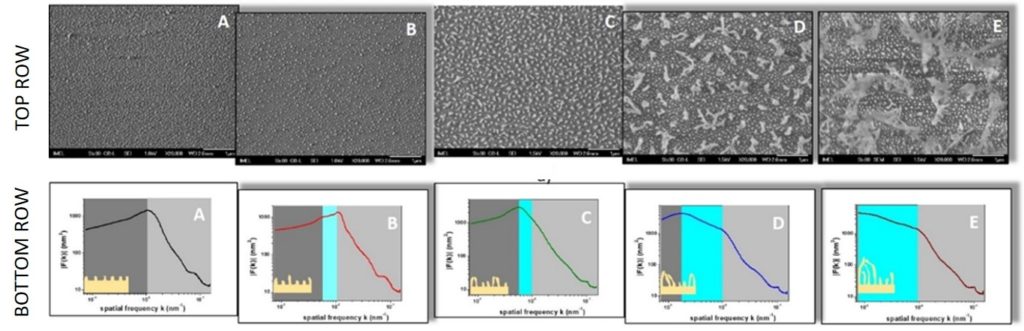
(a) Signal analysis (Fourier and Correlation analysis) for the identification and characterization of hierarchical surfaces (see Fig.6), 

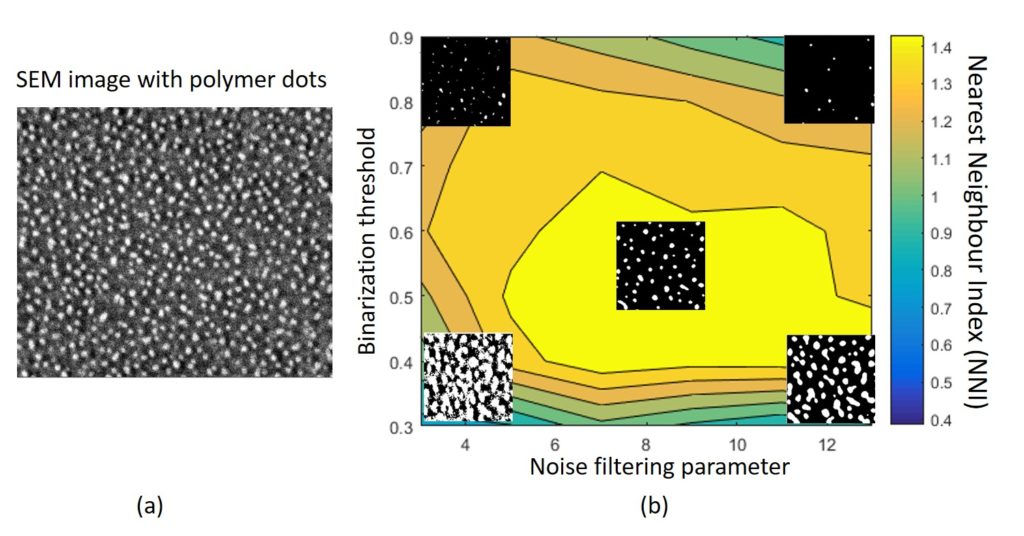
(b) Stochastic geometry (Point Pattern analysis), for the quantification of the extent of order/randomness of the positions of nanostructures (nanoparticles, nanodots, nanowires) on a substrate. Also, we investigated in detail the impact of image processing steps (denoising, binarization) on Nearest Neighbour Index in real SEM images with back-scattered and secondary electrons (see Fig.7).

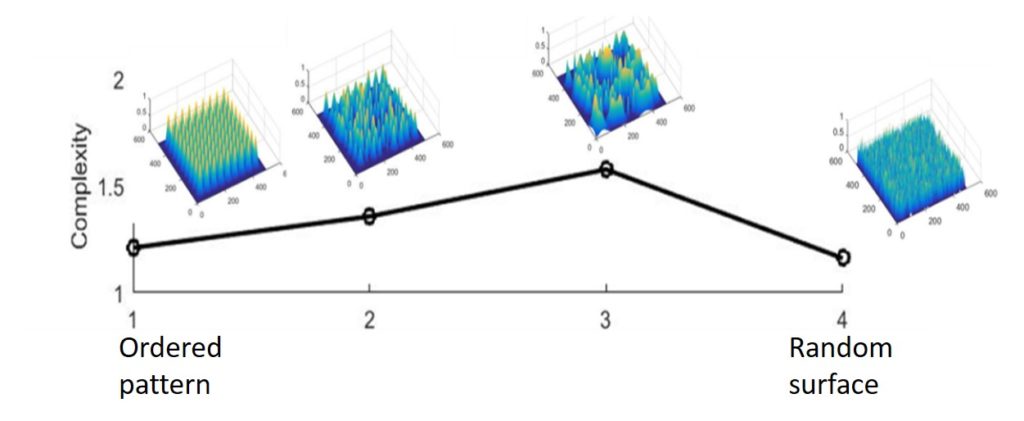
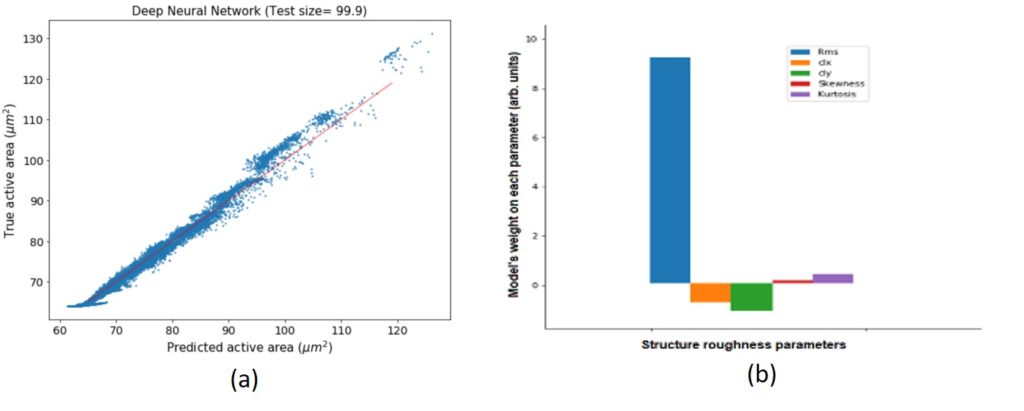
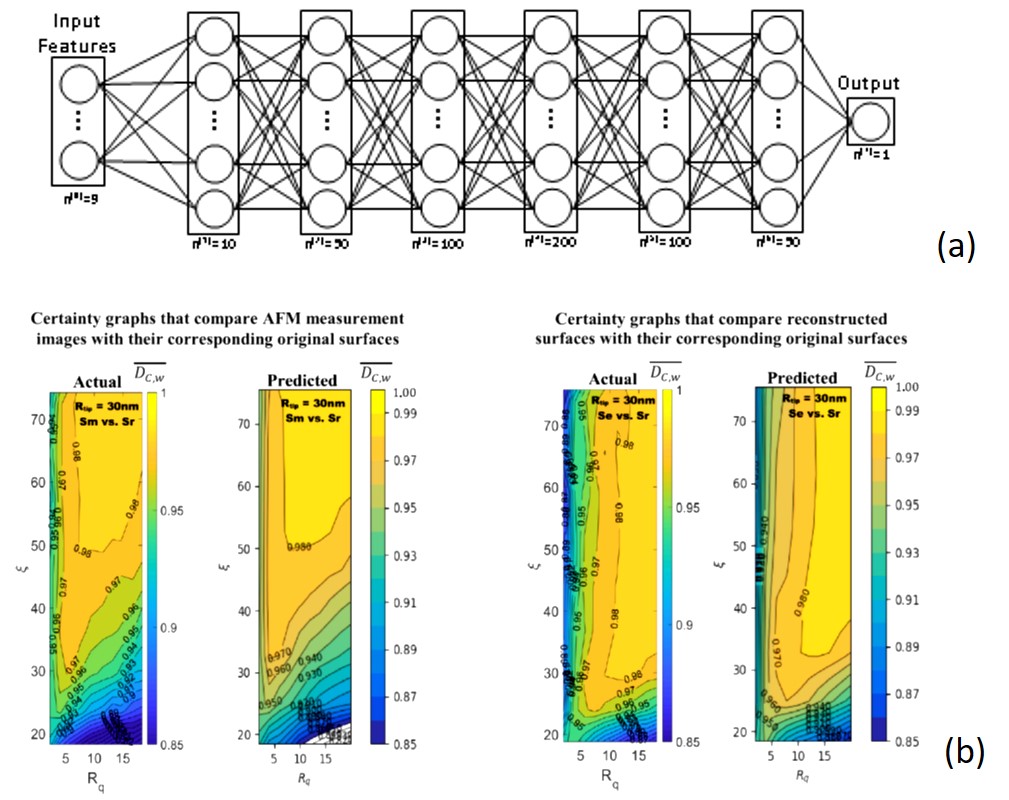
(c) Complexity science (multiscale entropies, multifractality) for measuring the complexity of nanostructured surfaces using the concept of statistical/average symmetry. A symmetry-based analysis has also been developed to characterize the deviation of nanostructure morphologies from perfect translational and scaling symmetries (see Fig.8).(e) Machine learning (neural networks, random forests) in order to link surface morphology to surface functionality (see Fig.9). Artificial neural networks have also been used to evaluate the importance of tip effects in the accuracy of surface roughness measurement with Atomic Force Microscope (see Fig.10).

TOP ROW: Top-down SEM images of PMMA surfaces etched by O2 plasma in our new homemade plasma nanotechnology equipment running the “etch-grass” process and having the capacity to control inhibitor flux. The surfaces exhibit a wide diversity of morphologies ranging from single-level (almost periodic) surfaces (A) under limited inhibitor flux, to hierarchical surfaces with varying types of hierarchy (amplitude or spatial) (B-E) induced by the inhibitor deposition with rate increasing from B to E. BOTTOM ROW: The radially averaged Fourier spectra of the SEM images shown in TOP ROW which demonstrate the frequency footprint of hierarchical morphologies as well as the ability of our technique to control the degree (frequency range) of the middle frequency scale of morphological hierarchy.  The insets in the diagrams of Fourier spectra are schematic drawings of the profiles of the etched surfaces to facilitate visualization.

Fig.7. (a) Top-down SEM image of polymer nanodots created after O2 plasma etching for 1min, (b) contour graph illustrating the dependence of the Nearest Neighbour Index (NNI) of nanodot positions on the noise smoothing filter and the binarization threshold needed to detect the dots. One can notice the broad maximum region (yellow area) where NNI gets its maximum value (~1.4) and the identification of nanodots is more accurate. At the four corners of diagram, the nanodot detection is deteriorated as shown in the inset binary images.

Fig.8. The proposed complexity measure versus the randomness of the positions and sizes of Gaussian mounds in a rough surface. One can notice the maximum of complexity measure at the most heterogeneous surface lying between full order and full randomness.

Fig.9. (a) Demonstration of the success of the Deep Neural Network to predict the actual surface area from the values of roughness parameters (Rms, correlation length clx, correlation length cly, skewness, kurtosis) of rough surfaces, (b) the evaluation of the significance of roughness parameters with respect to their impact on active surface area.

Fig.10. (a) Neural Network architecture used to predict the significance of AFM tip effects on the measurement accuracy of surface roughness. The input features may be the roughness parameters (rms Rq, correlation length ξ, fractal dimension, …) and the output result is the measurement certainty quantifying the significance of tip effects (low certainty, large tip effects). (b) Actual certainty graphs (left of each pair) and predicted from the neural network of (a) certainty graphs (right of each pair) for Rtip = 30nm over a range Rq and ξ values for surfaces with Gaussian height distributions. Both certainty graphs include instrumentation noise. One can clearly notice the success of the neural network predictions which can be used to quantify the impact of AFM tip effects and trigger actions for their correction if needed.

Skip to content